ЧАСТОТНО-градієнтних ПРИРОДА відцентрових сил

Гришаев А.А.

Інститут метрології часу і простору, ДП ВНИИФТРИ

141570 Московська обл., Менделєєве

Відцентрові сили - реальні сили.

Уявлення про силах, що діють на тіло при його русі по криволінійній траєкторії, до сих пір залишаються одним з найбільш заплутаних питань у фізиці. Вважають, що рівномірний рух тіла по колу завжди забезпечується єдиною результуючої силою - центростремительной: так, при русі супутника по круговій орбіті роль цієї сили грає сила тяжіння (возмущающими факторами нехтуємо). Рух тіла, яке обертають за допомогою центрифуги, теж, як вважають, відбувається під дією тільки центростремительной сили. Але традиційна динаміка, підходячи з однією міркою і до супутника, і до тіла в центрифузі, безсила пояснити принципову різницю в їх станах по частині механічних деформацій: тіло в центрифузі їх відчуває, а супутник - немає.

Теоретичні проблеми ще більше поглиблюються, коли рівномірний рух тіла по колу намагаються описати в системі відліку, що обертається з тією ж кутовою швидкістю і навколо тієї ж осі, що і тіло. У цій системі відліку швидкість і прискорення тіла дорівнюють нулю; як вважають, це є результатом компенсації центростремительной сили відцентровою силою. Відцентрова сила вважається однією з різновидів сил інерції, які слід брати до уваги при аналізі динаміки явищ лише в неінерційних системах відліку, в даному випадку - в обертовій. Хибність цієї концепції з очевидністю демонструється хоча б тим фактом, що при виході літака з піке відцентрова сила вдавлює льотчика в сидінні незалежно від того, в який з систем відліку аналізується цей процес.

Дійсно, якщо на тіло діє реальна сила, то мають місце реальні наслідки: тіло набуває прискорення або деформується. Такі слідства мають абсолютний, що не залежить від системи відліку характер, тим більше що вони супроводжуються тим чи іншим перетворенням енергії. Що ж стосується так званих сил інерції, які діють в одній системі відліку і в той же час не діють в інший, то вони є, на наш погляд, теоретичної фікцією, яку породжує невдалим вибором системи відліку. На відміну від цієї фікції, відцентрові сили є силами реальними.

Яка ж природа цих сил? Зауважимо, що якщо в пробному тілі має місце градієнт прискорень, з якими рухаються різні елементи тіла, і при цьому форма тіла і стан його руху не змінюються, то це означає, що дія градієнта прискорень якимось чином скомпенсировано. Зокрема, при обертанні диска з постійною кутовою швидкістю w навколо своєї головної осі має місце радіальний градієнт прискорень, і його дія скомпенсировано якраз відцентровими силами. Якщо ці сили не є механічними, то чи не можуть вони мати частотно-градиентную природу, як і сили тяжіння [1,2]? Знайдемо залежність для відповідного радіального розподілу частот у разі обертового диска. З формули для прискорення, яке набуває пробне тіло в умовах локального градієнта частот [3], ми отримуємо для градієнта цього прискорення вираз:

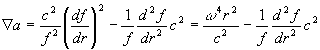, (1)

де

- радіус обертання, c - швидкість світла у вакуумі. Відкидаючи, в нерелятивістському наближенні, перший доданок, прирівняємо Ñ a радіальному градієнту прискорень, рівному w 2. Проинтегрируем отримане рівність по r і потім вирішимо результуюче диференціальне рівняння із перемінними; тоді для радіального розподілу частот отримаємо такий вираз:

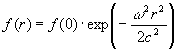. (2)

Як випливає з (2)

, Власні частоти квантових осциляторів в обертовому диску зменшуються в міру зростання радіуса, так що елементи диска, що обертається відчувають відцентрове прискорення

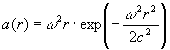, (3)

яке в нерелятивістському наближенні одно добре відомої величиною w

2 r.

Отже, припущення частотно-градієнтної природи відцентрових сил виглядає, на наш погляд, цілком розумним. Прийняття цієї гіпотези дозволяє, нарешті, пояснити, звідки беруться сили, які

, Через власного обертання Землі, зменшують вагу тел на екваторі в порівнянні з їх вагою на полюсі, а також ті сили, які викликають океанський прилив, що переміщається в протифазі з соняшниковою припливом. Ще в школі нас учили, що приплив, протифазний підмісячного, обумовлений відцентровими силами - завдяки обертанню Землі навколо центру обертання системи Земля-Місяць з періодом в місячний місяць. Але природа цих реальних сил, що викликають енергопревращенія планетарного масштабу, до сих пір залишалася загадкою.

Відцентрові сили і властивості гіроскопа.

Облік дії відцентрових сил дозволяє легко пояснити дивовижні реакції гіроскопа на зусилля, які прагнуть змінити просторову орієнтацію його осі обертання.

Перш за все слід усвідомити, що в обертовому з постійною кутовою швидкістю гіроскопі, до якого не прикладений відхиляє момент сил, має місце точна взаємна компенсація центростремительной і відцентрової сил, що діють на кожен елемент dm гіроскопа. Ця теза суперечить ортодоксальному підходу, згідно з яким для руху тіла по колу потрібно ненульова результуюча сила, спрямована до центру, яка постійно змінює напрямок вектора швидкості тіла. Але зауважимо, що такий підхід справедливий лише в умовах відсутності частотних градієнтів, тобто коли простір-час "плоске". В умовах же радіального розподілу частот (2) рух елемента dm по ізочастотной траєкторії, тобто по колу, відбувається саме тоді, коли частотно-градієнтні відцентрові сили врівноважуються доцентровими силами пружних деформацій.

Тепер стає очевидно, яким чином забезпечується стійкість орієнтації площини обертання гіроскопа. При щонайменшій зміні цієї орієнтації порушується компенсація сил: доцентрові вектори повертаються так, щоб бути спрямованими до центру обертання, а відцентрові вектори зберігають свої напрямки, нормальні до колишньої осі обертання. В результаті виникає повертає момент сил. Визначення гіроскопа має не просто містити поняття "швидко обертається тіло" - швидко в порівнянні з чим? - визначення повинно обумовлювати, що такий-то відхиляє момент сил компенсується повертає моментом сил при відхиленні площині гіроскопа не більше ніж на такий-то малий кут a.

Насправді, звичайно, картина трохи складніше: в результаті спільної дії відхиляють і повертають сил тонкий дискообразний гіроскоп згинається так, що його перетин площиною, що містить вісь обертання і силу, що відхиляє вісь, являє собою тангенсоіду. Але при малому куті a цим вигином можна знехтувати. Тоді з умови рівності модулів відхиляє і повертає моментів слід, що

Fl = J w 2 × tg a, (4)

де

F

- система, що відхиляє сила, l - відстань від точки прикладання сили F до центру інерції гіроскопа, J - момент інерції гіроскопа, і w - кутова швидкість його обертання. Взаємна компенсація цих двох моментів сил призводить до нульового кутовому прискоренню площині гіроскопа в напрямку відхилення; обнуління ж кутової швидкості відхилення відбувається якраз за допомогою прецесії - рівномірного обертання площини гіроскопа в ортогональному напрямку. Прирівнюючи поперечні складові - через відхилення і через прецесії - у лінійних швидкостей елементів гіроскопа, ми отримуємо для кутової швидкості прецесії W просте співвідношення:

W = w × sin a. (5)

При малому куті a, з урахуванням (

4), зі співвідношення (5) слід добре відомий вислів для кутової швидкості прецесії.

Вищевикладене пояснення властивостей гіроскопа, а, значить, і принципів, на яких ґрунтуються його різноманітні технічні застосування, на наш погляд, вигідно відрізняється від традиційного підходу, що ототожнює гіроскопічні сили з силами Коріоліса, які потрібно враховувати лише в обертових системах відліку, в той час як в невращающихся системах відліку вони дорівнюють нулю. Навпаки, відцентрові сили, як і вироблені ними дії, які не залежать від того, в який з систем відліку аналізується процес. Ми стверджуємо, що силові дії гіроскопів обумовлені ні чим іншим, як діями саме відцентрових сил, так чи інакше трансформованими відповідно до конструкції гироскопического пристрою і з доданими до неї зовнішніми зусиллями.

Відцентрові сили і рух супутників.

Вище йшлося про відцентрових силах для випадків, коли траєкторія пробного тіла формується при неодмінному участі будь-яких механічних сил, що викликають механічні деформації. У цих випадках відцентрове прискорення ортогонально вектору швидкості пробного тіла і дорівнює квадрату цієї швидкості, діленому на радіус кривизни траєкторії.

Принципово інакше проявляється відцентрове прискорення в випадках, коли механічні сили не діють на пробне тіло, і його рух визначається лише частотно-градієнтними силами - зокрема, силою тяжіння. Ця принципова різниця обумовлена ​​тим, що пробне тіло спочатку знаходиться на частотному схилі, причому ізочастотние, тобто Еквіпотенціальна, лінії є кривими. При цьому швидкість тіла v можна розкласти на дві складові: на тангенціальну vt, яка спрямована по дотичній до еквіпотенційної лінії в поточній точці знаходження тіла, і на радіальну vr, яка ортогональна цієї дотичної. Можна бачити, що градієнт прискорень елементів пробного тіла, що обумовлює появу відцентрового градієнта частот, визначається локальним градієнтом частотного схилу, і тому відцентровий градієнт частот визначається лише тангенціальною складової швидкості. При цьому відцентрове прискорення протилежно прискоренню через тяжіння і дорівнює квадрату тангенциальной швидкості, діленому на радіус кривизни еквіпотенційної лінії (тому відцентрове прискорення артилерійського снаряда мізерно: воно визначається не радіусом кривизни його траєкторії, а, фактично, радіусом Землі). Отже, сумарний градієнт частот в обсязі пробного тіла залежить не від повної його швидкості, а від тангенциальной - зокрема, коли вона дорівнює першої космічної швидкості, результуючий градієнт частот дорівнює нулю.

Здавалося б, ми прийшли до протиріччя: нульовий градієнт частот означає нульову результуючу частотно-градиентную силу; яка ж сила змушує тіло рухатися по колу? На наш погляд - ніяка; в даному випадку її і не потрібно. Дійсно, уявімо, що пробне тіло може рухатися лише по площині, на якій є однорідний градієнт потенціалу, тобто Еквіпотенціальна лінії є паралельними прямими. Якщо тіло рухається по еквіпотенційної лінії, то це означає, що сила, обумовлена ​​градієнтом потенціалу, скомпенсирована якийсь інший силою. Чи справедливий цей принцип при іншій геометрії поля? Нехай, наприклад, еквіпотенціальні лінії є концентричними колами. Якщо швидкість тіла досить мала, щоб "відчувати" неоднорідність поля, то названий принцип залишається справедливий: тіло рухається по еквіпотенційної лінії, тобто по колу, якщо доцентрова сила, обумовлена ​​градієнтом потенціалу, скомпенсирована іншою силою, в нашому випадку - відцентрової. Більш того, саме протиборство центростремительной і відцентрової сил забезпечує радіальну стійкість руху тіла: при відхиленні значення радіусу від "рівноважного" виникає ненульовий градієнт частот в тілі, що виправляє відхилення. Знаходить своє тривіальне пояснення і "парадокс супутника" [4,5]: для того, щоб збільшити кутову швидкість супутника на круговій орбіті, супутник буде ... пригальмувати, і навпаки.

Які ж орбіти супутників дає викладається тут підхід? У найпростішому випадку руху тіла в сферично-симетричному полі, поточний радіус кривизни еквіпотенційної лінії дорівнює поточному радіус-вектору R. Якщо вважати поле тяжіння Землі ідеально сферически-симетричним, то, з урахуванням вищевикладеного, аналітичні вирази, в циліндричних координатах (R, j), для одного кроку чисельного інтегрування орбіти мають вигляд:

j 1 = j 0 + v t0 T / R 0; (6)

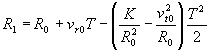; (7)

; (8)

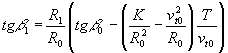; (9)

vt1 = v 1cos b 1; vr 1 = v 1sin b 1, (10)

де

T

(сек) - крок інтегрування, K - добуток маси Землі на гравітаційну постійну, b - кут між вектором швидкості і дотичній до еквіпотенційної лінії. Чисельне інтегрування за алгоритмом (6) - (10), в якому прямо враховується відцентрове прискорення (vt) 2 / R, дає кеплерівські орбіти, як і традиційний підхід, в якому відцентрове прискорення не враховується. Втім, багато авторів стверджують, що рух супутника в першому наближенні визначається лише силою тяжіння, але тут же додають наступне: "... величина першої космічної швидкості зменшується зі збільшенням висоти польоту. Це пояснюється тим, що поле тяжіння стає слабкішим, і потрібна менша відцентрова сила, щоб врівноважити силу тяжіння "[6]. Мабуть, подібні цитати слід розуміти буквально: хоча виявляються однаковими орбіти, що розраховуються в рамках як традиційного, так і викладається тут підходів, все-таки другий з них, на наш погляд, більш адекватний фізичної реальності.

Проілюструємо, наскільки просто і природно цей підхід пояснює дивну поведінку супутника, що зазнає власне обертання, вісь якого ортогональна площині орбіти. Таке обертальний рух, складаючись з орбітальним, призводить до градієнту тангенціальних швидкостей для різних елементів супутника. Результуюче зміна відцентрового прискорення D

нескладно оцінити. Нехай супутник має тангенціальну швидкість V при радіус-вектор R; нехай він має лінійний радіус r і обертається з кутовою швидкістю w. Тоді, в залежності від напрямку обертання,

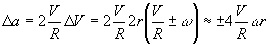. (11)

Як видно з (

11), приріст D a обумовлено лише складанням двох обертальних рухів, тобто воно має чисто кінематичне походження і не залежить, зокрема, від моменту інерції супутника. Наслідком збільшення відцентрового прискорення (1 + 1), є відповідне обурення орбіти. Наприклад, якщо супутнику повідомлена перша космічна швидкість в тангенціальному напрямку, то невелике збільшення відцентрового прискорення (1 + 1) робить результуючу орбіту еліптичної - з ексцентриситетом, рівним відношенню D a до прискорення вільного падіння. Так, якщо супутник двометрового радіусу робить один оборот в секунду, то для низьких орбіт цей ексцентриситет становить приблизно 0.0064. Зауважимо, що з традиційного підходу, в якому враховуються тільки сили тяжіння, не випливає, що обертається тіло повинно тяжіти інакше, ніж невращающейся.

Слід додати, що у планет не виявляється аналогічної залежності між власним обертанням і формою орбіти. Справа в тому, що ця залежність отримана при неявному допущенні того, що тіло, що обертається є структурно-статичним

[3] або, за термінологією Миколаївського [7], пасивно -тяготеющім об'єктом. Планети ж такими не є, оскільки вони мають власні частотні "провали" і діючі енергореактори в своїх надрах.

Висновок.

Спорідненість сил тяжіння і відцентрових сил помічено давно. Вельми ефектно це спорідненість демонструється досвідом з насінням, проростає на периферії обертового колеса: при досить швидкому обертанні паростки тягнуться до центру цього колеса. Напрошується висновок, що саме градієнт частот задає паросткам опорна напрямок в просторі. Цей висновок побічно підтверджується експериментами з пророщуванням насіння на орбітальних станціях. Як зазначалося вище, в разі кругової орбіти градієнт частот в обсязі станції дорівнює нулю, і тому нормальне проростання насіння порушується: поділ клітин відбувається не по виділеному напрямку, а безсистемно, що робить "паростки" виродками. Слід підкреслити, що невагомість не обов'язково супроводжується нульовим градієнтом частот. Так, нульовий градієнт частот не має місця в ліфті, вільно падаючому по вертикалі, а також в літаку, що рухається по "гірці" для отримання штучної невагомості, оскільки в цих випадках відсутня компенсація сили тяжіння відцентровою силою.

Отже, ми постаралися показати, в чому полягає сутність спорідненості сил тяжіння і відцентрових сил: і ті, і інші обумовлені градиентами власних частот квантових осциляторів в пробному тілі, хоча частотні градієнти, що забезпечують тяжіння, і відцентрові частотні градієнти створюються по-різному.

Маючи частотно-градиентную природу, відцентрові сили, по-перше, не викликають механічних деформацій і, по-друге, не здійснюють роботи в тому сенсі, що вони не повідомляють енергію тілу: вони перетворюють внутрішню енергію тіла в кінетичну - аналогічно тому, як це роблять сили тяжіння [1,2].

Автор дякує В.І. Беленко і А.В. Новосьолова за корисну дискусію.

Посилання.

джерело:

http://newfiz.narod.ru

Надійшло на сайт: 08 июня 2001.