Публікація в Інтернеті теплофізичних властивостей речовин: проблеми і рішення при роботі з таблицями

Очок В.Ф.

Журнал " праці Академенерго ", №2 2009

Викладено методику і інструментальні засоби публікації в Інтернеті інтерактивних розрахунків по теплофізичних властивостях речовин.

Таблиці теплофізичних властивостей речовин в довідковій літературі, як правило, публікуються в двох видах:

• теплофізичні властивості речовин на лінії насичення або при певному (найчастіше атмосферному) тиску: таблиці з «боковиком» - дискретні значення температури і наступними стовпцями - значеннями властивостей;

• теплофізичні властивості речовин в однофазної області: таблиці з «боковиком» - дискретні значення температури і «шапкою» - дискретні значення тиску.

Дані першого виду, як правило, укладаються в повністю заповнену таблицю, де в першому стовпці ( «боковику»), як уже зазначено, зберігаються значення температури, а в наступних - відповідні цим значенням температури значення теплофізичних властивостей речовин: тиск насичення, щільність, питома ізобарна теплоємність, питома ентальпія, питома ентропія, в'язкість (кінематична і динамічна), теплопровідність, число Прандтля і т.д. Табл. 1 - це типова подібна таблиця, взята з [1]. Вона зберігає теплофізичні властивості конденсату Карачаганакского газового родовища ( http: // ru. wikipedia. org / wiki / Карачаганакское_месторожденіе ).

Табл. 1. Типова таблиця за властивостями речовини на лінії насичення

Іноді дані першого виду в довідковій літературі представлені не повністю заповненими таблицями: щільність дана, наприклад, в одному температурному інтервалі або при одних значеннях температури, а теплопровідність в іншому інтервалі або при інших значеннях температури. Але ця особливість не є критичною як у випадку з даними другого виду (див. Нижче): при обробці таких «разноінтервальних» даних з таблиці вилучаються пари векторів (температура-щільність, температура-теплопровідність і т.д.) однакової довжини для подальшої сепаратної роботи з ними - інтерполяції або апроксимації.

Дані другого виду, як правило, розміщуються в частково заповнених таблицях, де прочерки в осередках означають, що при даних значеннях температури ( «боковик» таблиці) і тиску ( «шапка» таблиці) розглядається речовина знаходиться в іншому агрегатному стані. Табл. 2 - це типова подібна таблиця, взята також з [1] і відповідна того ж речовини, вірніше суміші речовин (вуглеводнів) - конденсат Карачаганаксого газового родовища.

Табл. 2. Типова частково заповнена таблиця за властивостями речовини в однофазної області

Дані, показані в табл. 2, в нижньому лівому кутку відсічені невидимою лінією, дискретні координати якої зберігаються в перших двох стовпчиках табл. 1 (температура і тиск насичення). В [1] наведені й інші таблиці, схожі за виглядом з табл. 2, але зберігають дані по іншим теплофізичних властивостях, перерахованим в «шапці» табл. 1.

Якщо ж таблиця другого виду заповнена повністю і при цьому «накриває» лінію насичення (фазового переходу), то в такій таблиці ступінчастою лінією відзначається межа фазового переходу «рідина - газ (кипіння - конденсація)», «рідина - тверда речовина (плавлення - кристалізація ) »або« тверда речовина - газ (сублімація - сублімація) ». Типовою повністю заповненою таблицею другого виду із ступінчастою лінією, що відокремлює воду від водяної пари є таблиця термодинамічних властивостей води і водяної пари в однофазної області (табл. 3), взята з [2].

Табл. 3. Фрагмент типовою повністю заповненою таблиці за властивостями речовини в однофазної області із ступінчастою лінією фазового переходу

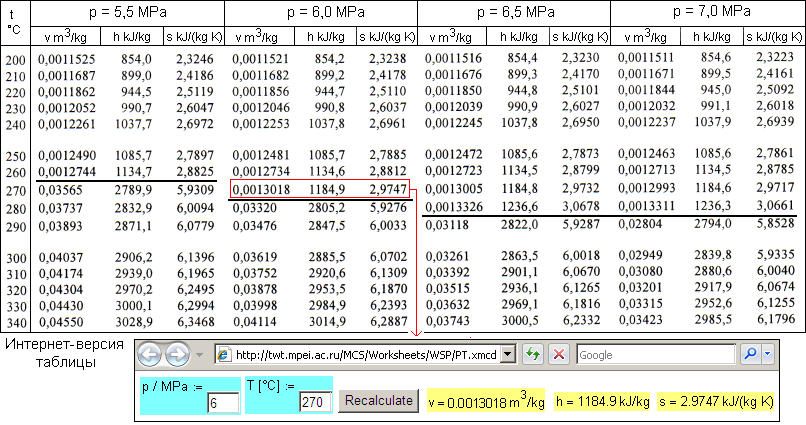
В даний час у зв'язку з розвитком технології «хмарних» обчислень і з урахуванням того факту, що комп'ютер з виходом в Інтернет на столі інженерно-технічного працівника все частіше і частіше замінює традиційний паперовий довідник з «мертвими» формулами, графіками, таблицями, стало можливим переносити таблиці, подібні до тих, які показані вище, на спеціальні розрахункові сайти Інтернету [3-5]. Так внизу табл. 3 читач може побачити її Інтернет-версію, розміщену за адресою http://twt.mpei.ac.ru/MCS/Worksheets/WSP/PT.xmcd .

Таблиці теплофізичних властивостей речовин, що публікуються в довідковій літературі, як правило, отримані в результаті розрахунку за формулами, які, в свою чергу, отримані через статистичну обробку експериментальних даних з опорою на деякі теоретичні положення. Якщо говорити про такий речовині як вода і водяна пара, то відповідні таблиці термодинамічних властивостей цього найважливішого теплоносія і робочого тіла (наприклад, таблиця 3) були отримані на основі розрахунків за відповідними формуляцій Міжнародної асоціації по властивостям води і водяної пари ( www . iapws. org ), Зокрема по формуляції IAPWS -IF 97 ( www.iapws.org/relguide/IF97-Rev.pdf ). Одним з автором цієї статті була пророблена робота з перекладу формул формуляції IAPWS -IF 97 (набір текстів і «мертвих» формул, оформлених в форматі pdf і які можна «скачати з сайту www.iapws.org/relguide/IF97-Rev.pdf ) В «живі» інтерактивні мережеві розрахунки [6-8] з використанням технології Mathcad Calculation Server (MCS) [9].

Невеликий відступ від основної теми (інтермедія).

Формули формуляції IAPWS -IF 97 охоплюють п'ять областей:

· Вода ( http://twt.mpei.ru/MCS/Worksheets/WSP/Region1.xmcd )

· водяна пара ( http://twt.mpei.ru/MCS/Worksheets/WSP/Region2.xmcd )

· Критична область ( http://twt.mpei.ru/MCS/Worksheets/WSP/Region3.xmcd )

· Водяна пара при високих температурах ( http://twt.mpei.ru/MCS/Worksheets/WSP/Region5.xmcd )

· Лінія насичення ( http://twt.mpei.ru/MCS/Worksheets/WSP/Region4p.xmcd і http://twt.mpei.ru/MCS/Worksheets/WSP/Region4t.xmcd )

Є і формуляція IAPWS -IF 95 ( www.iapws.org/relguide/IAPWS95.pdf ), В якій немає розбивки на окремі область, але внаслідок цього розрахунок ведеться по більш складним набором формул, які відкриті в Інтернеті за адресою http://twt.mpei.ac.ru/MCS/Worksheets/WSP/iapwsif95.xmcd .

У наведеному вище списку областей формуляції IAPWS -IF 97 прописані адреси відповідних сторінок Інтернету, зібраних на сайті http : // twt. mpei. ru / o chkov / WSPHB . Відкритість формул формуляції IAPWS-IF97 дозволяє легко їх програмувати. Дані формули були реалізовані в середовищі інженерного калькулятора Mathcad і опубліковані в Інтернеті за тієї самої технології MCS. На рис. 1 відображена сторінка сайту Інтернету, зайшовши на яку можна вибрати параметри осей X -Y графіка (це на рис. 1 не показано) і побачити конфігурацію даних областей (це на рис. 1 показано для графіків pT, Ts, Z (коефіцієнт стисливості) - ρ і 1 / Cp -ρ).

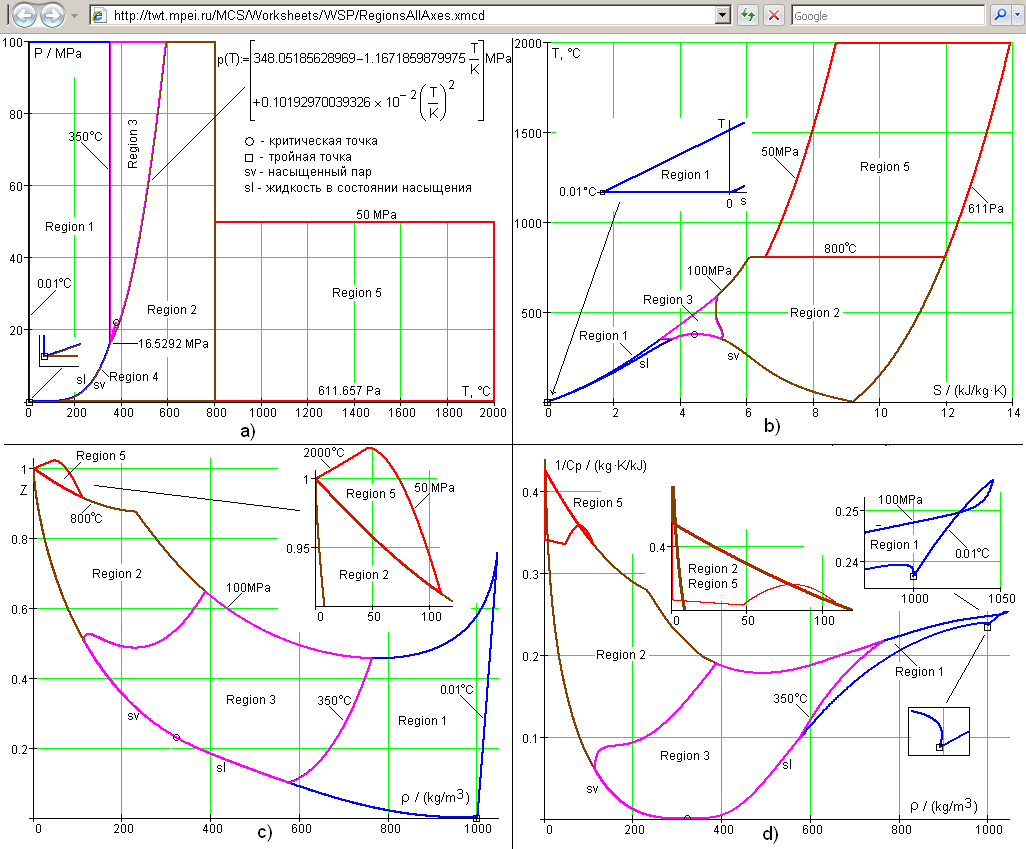
Мал. 1. Зміни областей формуляції IAPWS-IF97 в різних діаграмах

У верхньому лівому кутку рис. 1 (пункт a) показано традиційне «прямокутне» відображення конфігурації областей формуляції IAPWS-IF97 в рамках pT діаграми. У цій діаграмі область 4 згортається в одну лінію, що тягнеться від потрійної точки (273.16 K і 611.657 Pa) до критичної точки (647.096 K і 22.064 MPa). У верхньому правому куті рис. 1 (пункт b) конфігурація областей відповідає діаграмі, часто використовуваної для відображення паротурбінних термодинамічних циклів (Ts діаграма). Дві інші конфігурації областей (пункти c і d) використовуються рідше, але вони не менш цікаві. Діаграма z- ρ (коефіцієнт стисливості і щільність) показує, наскільки параметри води і водяної пари відрізняються від параметрів ідеального газу, у якого z = 1. Діаграма 1 / Cp -ρ (величина, зворотна значенням питомої ізобарно теплоємності, і щільність) примітна тим , що на ній кордони областей утворюють якісь петлі, зміст яких можна зрозуміти при переході від плоских до об'ємним діаграм [10-11], де виявляється хибність цих перетинів.

На рис. 2 як приклад показана одна зі сторінок сайту http : // twt. mpei. ru / o chkov / WSPHB , Де не тільки дано набір формул, за якими ведеться розрахунок термодинамічних властивостей води і водяної пари в околокрітіческой області (область 3 формуляції IAPWS-IF97), але і здійснюється сам розрахунок з висновком «на друк» всіх підсумкових і проміжних результатів.

Мал. 2. Мережевий розрахунок по формуляції IAPWS-IF97 для області 3 (околокрітіческая область)

Але повернемося до теми нашої статті - до розрахунків за таблицями, а не за формулами.

Коли в довідковій літературі опубліковані формули для розрахунку теплофізичних властивостей речовин, то їх нескладно запрограмувати і поширювати серед користувачів або у вигляді пакету програм, якщо необхідно мати в своїх прикладних програмах відповідні функції і / або процедури (див., Наприклад, сайт www. wpu. ru , Якщо мова йде про воду, водяній парі, газах і газових сумішах - робочих тілах теплоенергетики), або у вигляді сторінок сайтів Інтернету (див. Вище), якщо потрібні тільки разові розрахунки. Так (продовження вищевикладеного відступу), зайшовши на сторінку Інтернету з адресою http : // twt. mpei. ru / MCS / Worksheets / WSP / PT. xmcd , Можна розрахувати теплофізичні властивості води і водяної пари в залежності від заданих значень тиску і температури (мережевий аналог табл. 3). При цьому значення тиску і температури можуть приймати будь-які значення в рамках, показаних в пункті a на рис. 1, а не дискретні, зафіксовані в «боковику» і «шапці» табл. 3. Більш того, зайшовши на сторінки Інтернету з адресами http : // twt. mpei. ru / MCS / Worksheets / WSP / P H. xmcd або http : // twt. mpei. ru / MCS / Worksheets / WSP / PS. xmcd , Можна вирішити зворотні завдання - розрахувати теплофізичні властивості води і водяної пари в залежності від заданих значень тиску і питомої ентальпії або питомої ентропії (закінчення відступу).

Але дуже часто в довідковій літературі інформаційним ядром є саме таблиці, а не відповідні їм формули. Чому !?

По-перше, нерідко ніяких формул немає і не було, а в таблицях подано результати тестування речовин на предмет визначення їх теплофізичних властивостей без особливої ​​обробки отриманих даних. У таких випадках часто публікують не таблиці, а графіки з кривими, поблизу яких проставлені експериментальні точки. На графіках чітко видно ті чи інші залежності властивостей речовин від їх параметрів (див., Наприклад, рис. 1, 9 та 10). Прийоми перекладу графіків в таблиці викладені в розділі 3 монографії [5].

По-друге і головне, часто виявляється так, що формули в довідковій літературі є і навіть у надлишку, але скористатися ними буває практично неможливо. Справа в тому, що опис формул в деяких монографіях довідкового характеру, дано так заплутано, що виключається їх практичне використання для написання програм не тільки читачами, але, мабуть, і самими авторами. Така «формульна плутанина» утворюється «вільно чи мимоволі». «Мимоволі» ймовірно тому, що багато книги пишуться уривками різними авторами авторського колективу в різний час. Такі книги часто не мають загального наукового редагування, що включає принцип: «Якщо в книзі є формула, то по ній можна і потрібно вважати!». У таких книгах часто відсутні деякі коефіцієнти формул і читач повинен шукати їх в інших джерелах, а також не дано чітких обмежень щодо використання формул і т.д. «Свідомо» плутанина в формулах в деяких особливих випадках виходить тому, що автори вже мають комерційну програму розрахунку по описуваних формулами і не хочуть плодити конкурентів, але в той же час мають намір прорекламувати свої напрацювання.

У будь-якому випадку відмова від використання формул і перехід до розрахунків, заснованим на рейперних точках опублікованих таблиць, має ще одне важливе підставу.

Розрахунок за формулами іноді буває занадто тривалим, що в ряді випадків не задовольняє користувачів. Приклад - створення комп'ютерних тренажерів для персоналу, який обслуговує теплоенергетичні об'єкти. Тут не потрібна особлива точність розрахунків теплофізичних властивостей робочих тіл цих об'єктів у всьому діапазоні робочих параметрів (див. Рис. 1), а необхідний тільки швидкий рахунок в режимі реального часу за програмою, яка працює в обмеженому діапазоні вихідних параметрів за нескладним алгоритмом, наприклад, по лінійної інтерполяції. Або інтерполяції сплайнами, а також апроксимації - методами, описаними нижче.

В інженерному калькуляторі Mathcad є вбудовані засоби вирішення завдань інтерполяції та апроксимації. На рис. 3 показана сторінка Інтернету, на якій за технологією MCS викладений Mathcad-документ з обробкою даних, показаних в табл. 1.

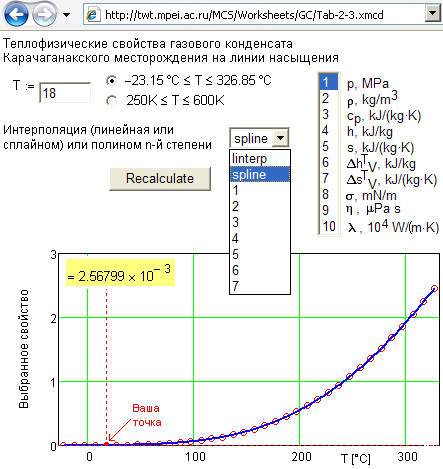
Мал. 3. Сайт Інтернету за розрахунком властивостей речовини на лінії насичення

Відвідувач сайту вказує потрібну йому температуру в зазначених діапазонах за шкалою Цельсія або Кельвіна, вибирає зі списку потрібне йому теплофізичних властивостей даного газового конденсату, зазначає потрібний спосіб обробки табличних даних (linterp - лінійна інтерполяція, spline - інтерполяція сплайном, 1-7 - апроксимація поліномом 1 , 2, ... 7-го ступеня), натискає кнопку Recalculate і отримує відповідь числом (відповідна одиниця виміру відзначена в списку параметрів) і графіком з інтерполюючої або апроксимуючої лінією, «нанизаної» на неї т окулярами з вихідної таблиці. Якщо ж була обрана апроксимація поліномом n-го ступеня, то додатково (це на рис. 3 не показано) видаються значення коефіцієнтів даного полінома.

Інтерполяція сплайнами, яка застосовується для обробки даних з табл. 1 (рис. 3), показана нижче на рис. 9 для пари параметрів: температура і тиск насичення.

Функцію не однієї, а вже двох змінних, з опорою нема на два вектора, а на матрицю значень властивостей речовин також нескладно згенерувати в середовищі Mathcad. Стандартні засоби цього пакета - вбудовані функції виду * spline вимагають, щоб матриця вихідних даних (у нас це значення щільності) для вже двовимірної сплайн-інтерполяції була повністю заповнена і квадратна. При цьому значення аргументів (у нас це значення температури і тиску) повинні зберігатися в додаткової матриці з двома стовпцями. А наша відповідна матриця не повністю заповнена і не квадратна - див. Табл. 2.

Проблему незаповненості матриці можна вирішити через додаткову її обробку, через допоміжну інтерполяцію - см. Рис. 4.

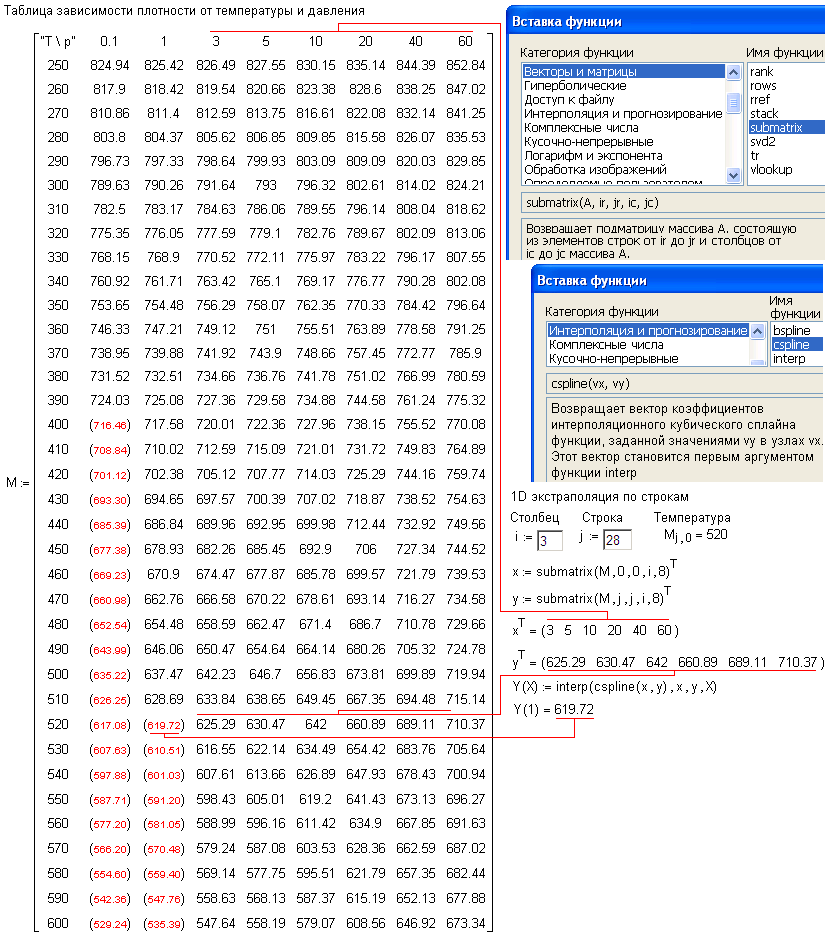
Мал. 4. «Штучне» заповнення частково заповненою матриці

На рис. 4 показано, як за допомогою допоміжної сплайн-інтерполяції, вірніше, екстраполяції порожні місця вихідної матриці (таблиці 2) заповнюються якимись ерзац-значення, які не будуть потім використані, але які допоможуть нам провести інтерполяцію за реальними точкам. Сенс слова «ерзац» тут в тому, що ми в цей діапазон надалі потрапляти не повинні, але ці «ерзац-значення» допоможуть нам провести інтерполяцію біля кордону фазового переходу. На рис. 4 ці значення відзначені дужками, більш дрібним шрифтом і іншим (червоним) кольором. При цій операції заповнення матриці можна додатково вести контроль правильності вихідних даних. На рис. 5 показаний додатковий графік, що фіксує аномальний елемент матриці М28, 5.

Мал. 5. Фіксація помилки введення матриці

Ця аномалія (помилка, помилка) є наслідком або декількох невдалих спроб ввести числа при ручному введенні матриці або при збої распознавателя текстів при обробці відсканованого малюнка матриці, або могла бути у вихідній таблиці. Так чи інакше ця помилка (606.89) була виправлена ​​(660.89) - порівняйте рис. 4 і 5.

Після операції введення ерзац-значень (рис. 4) у нас виходить повністю заповнена, але не квадратна матриця. Проблему «квадратности» матриці можна вирішити двома способами:

· Вставкою в неквадратні матрицю додаткових стовпців або рядків, елементи яких згенеровані знову ж через інтерполяцію;

· Зведенням однієї двомірної інтерполяції до двох одновимірним інтерполяції, що ми і зробимо.

На рис. 6 показано створення функції з ім'ям z з двома аргументами t і p, що реалізує сплайн-інтерполяцію даних, що зберігаються в матриці М. Для цього:

1) через вбудовану в Mathcad функцію submatrix з матриці М вилучаються: вектор Т (дискретні значення температури - «боковик» таблиці 2), вектор Р (дискретне значення тиску - «шапка» таблиці) і матриця z (значення щільності конденсату при відповідних значеннях температури і тиску; подматріца при цьому транспонується);

2) циклом for (циклом з параметром i - номер стовпчика) з одним оператором в тілі генерується додатковий вектор z ', який зберігає значення щільності конденсату в проміжних точках (перша одномірна сплайн-інтерполяція по тиску);

3) за отриманими проміжним точкам (вектор z ') стоятся підсумкова (друга) сплайн-інтерполяція по температурі.

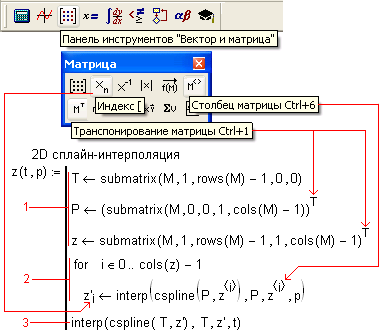
Мал. 6. Реалізація двомірної інтерполяції через дві одновимірні

Технологія двох одновимірних інтерполяцій замість однієї двомірної має ту перевагу, що можна в цих двох інтерполяції комбінувати методи, застосувати, наприклад, в першій інтерполяції інтерполяцію сплайнами, а в другій лінійну інтерполяцію. Це дозволити в ряді випадків уникнути такого «батога» інтерполяції як осциляції (коливань) між вузлами сітки інтерполяції. Крім того, такий поділ дає можливість більш широко комбінувати методи обробки табличних даних, застосовувати, наприклад, по одному аргументу інтерполяцію, а по іншому - апроксимацію.

При виведенні відповіді «на друк» за допомогою функції if (рис. 7) відсікаються відповіді, вихідні дані для яких виходять за рамки допустимих.

Мал. 7. Оператори, підготовки відповіді до висновку «на друк»

При формуванні відповіді (див. Рис. 7) враховуються не тільки прямокутні кордону таблиці значень щільності (табл. 2: 250-600 K по температурі і 0.1-60 MPa по тиску), але і лінія початку кипіння - см. Рис. 8, який також розміщений в Інтернеті і на який є відповідна посилання з області завдання вихідних значень температури і тиску (див. Рис. 8). Якщо вихідні дані виходять за рамки допустимих, то змінним, які видає «на друк», присвоюється не чисельне значення, значення спеціальної змінної NaN (N ot a N umber - не числом). Але ці обмеження потрібно буде зняти, якщо функція z (t, p), буде використовуватися для розв'язання оберненої задачі, для чисельного визначення, наприклад, температури по тиску і щільності або тиску, по температурі і щільності. В цьому випадку при реалізації ітерацій допустимо виходити за рамки значень температури і тиску, окреслених на рис. 8. Тут, правда, лінійна інтерполяція НЕ буде годитися, тому що похідна від цієї функції є константою. Спла-ітерполяція тим і хороша, що відповідні функції мають першу і втору похідні, що часто буває необхідно при реалізації різних чисельних методів: методу Ньютона пошуку коренів або методу градієнтного спуску при пошуку мінімуму.

У розрахунку використовуються невидимі змінні (це допустимо в середовищі Mathcad: змінні з білим кольором шрифту на білому фоні), що спрощує читання підсумкового документа (див. Рис. 10 нижче). Змінні-діапазони з іменами tt і pp будуть аргументами при побудові графіків.

Мал. 8. Область допустимих значень температури і тиску для інтерполяційної функції

На графіку, показаному на рис. 8, як зауважив читач, шкала абсцис перевернута: низькі температури знаходяться вгорі, а високі внизу. Це зроблено навмисно для того, щоб візуально наблизити даний графік до відповідної йому таблиці 2. Так склалося історично, що в «боковик» таблиць числові значення (значення температури, якщо мати на увазі табл. 1, 2 і 3) майже завжди збільшуються зверху вниз, а на осях ординат графіків - від низу до верху. На рис. 8 ця традиція порушена.

На рис. 7 було показано закінчення згорнутої області, а на рис. 9 її початок.

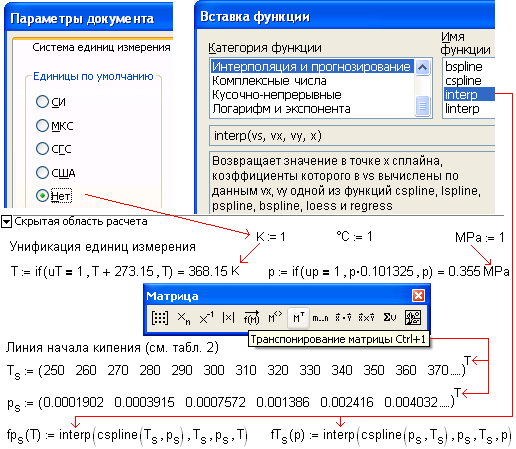
Мал. 9. Початок згорнутої області розрахунку щільності газового конденсату

На рис. 9 показані, оператори, по-перше, що враховують різні одиниці вимірювання при введенні вихідних даних, і по-друге, здійснюють через одновимірну сплайн-інтерполяцію формування двох функцій користувача: функцію fps (T) і fTs (p) - пряму і зворотну функцію залежності тиску і температури початку кипіння, які будуть використані (див. рис. 7) для контролю знаходження вихідних даних в обумовленому діапазоні (див. рис. 8).

Після всіх перерахованих вище дій отримана і опублікована в Інтернеті сторінка, показана на рис. 10.

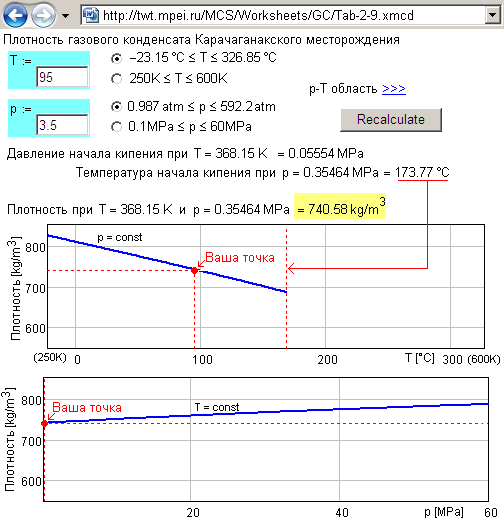
Мал. 10. Сторінка Інтернету з інтерактивним розрахунком щільності газового конденсату

На сторінці Інтернету, показаної на рис. 10, є посилання на сервер, з якого можна завантажити відповідну функцію, що повертає щільність газового конденсату. Цю функцію можна вставити в власний Mathcad -Розрахунок і працювати автономно без виходу в Інтернет. Відповідні функції можна створити і з використанням традиційних мов програмування (BASIC, Pascal, C та ін.), Маючи під рукою відкритий код розрахунку. Це ще одна причина, чому в нашому розрахунку не був задіяний повною мірою інструментарій фізичних величин і одиниць їх вимірювання, вбудований в пакет M athcad [12] - в «традиційних мовах програмування» цих коштів немає.

На рис. 10, показано, що не тільки виводиться розраховане числове значення щільності газового конденсату в залежності від заданих значень температури і тиску, але показані також ізобара і ізотерма, що дозволяє прогнозувати зміну даного властивості при зміні зовнішніх умов. Функцію двох аргументів можна було також відобразити і поверхнею, а не тільки двома ізолініями (ізобара і ізотерма), але ми цього не робимо з двох причин. По-перше, при публікації Mathcad-документів в Інтернеті за технологією MCS, як правило, не можна міняти орієнтацію поверхні в віртуальному просторі екрану дисплея для знаходження кращого ракурсу. І по-друге, теплофізичні властивості речовин, а особливо сумішей речовин, залежать не від двох, а від трьох і більше параметрів, і їх уже не можна відобразити графічно поверхнею. Тут можна використовувати тільки ізолінії. Мал. 11 ілюструє цю тезу.

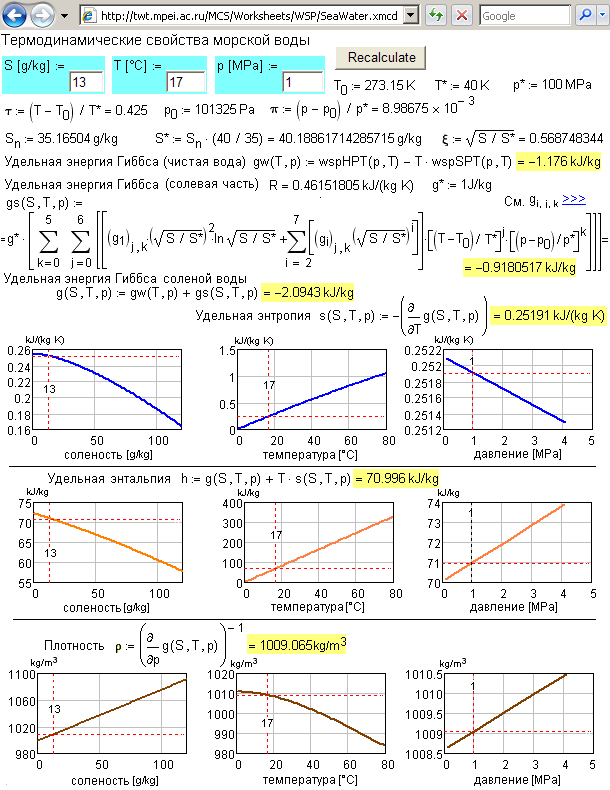
Мал. 11. Сторінка Інтернету з інтерактивним і відкритим розрахунком теплофізичних властивостей морської води

Висновок:

При виконанні інноваційної освітньої програми ( http://inedu.mpei.ru ), Що проводиться Московським енергетичним інститутом ( www.mpei.ru ) В рамках вирішення проблеми передачі знань від покоління до покоління [13] і розвитку Електронної енциклопедії енергетики ( www.trie.ru ), Були створені сторінки Інтернету, на яких ведеться розрахунок теплофізичних параметрів більш ніж 3000 речовин, сумішей речовин, металів, сплавів та інших матеріалів, що застосовуються в енергетиці як робочу силу тіл, теплоносіїв, конструкційних матеріалів і т.д. Доступ до цих станицях відкритий через Інтернет-версію п'ятого тому [5] довідкової серії «Теплоенергетика і теплотехніка» [14]. адреси http : // twt. mpei. ru / TTHB .

література:

1. Григор'єв Б.А. Теплофізичні властивості та фазові рівноваги газових конденсатів і їх фракцій / Б.А. Григор'єв, А.А. Герасимов, Г.А. Ланчак; під заг. ред. Б.А. Григор'єва. - Видавничий Дім МЕІ, 2007

2. Александров А.А., Григор'єв Б.А. Таблиці термодинамічних властивостей води і водяної пари. - М .: Изд. МЕІ, 1999.

3. Очок В.Ф. Теплотехнічний довідник в Інтернеті // Нове в російській електроенергетиці, № 5, 2005

4. Очок В.Ф. Математичні пакети і мережевий інтерактивний теплотехнічний довідник: проблеми та рішення // Теплоенергетика, № 6, 2006

5. Очок В.Ф. Інтернет-версія довідника Теплоенергетика і теплотехніка. Інструментальні засоби створення і розвитку / Г.Ю. Кондакова, А.С. Копилов, К.А. Орлов та ін. - Видавничий Дім МЕІ, 2007 (видання випущено за фінансової підтримки Російського фонду фундаментальних досліджень www. Rffi. Ru)

6. Александров А.А. Теплофізичні властивості води і водяної пари в Інтернеті / А.А. Александров, В.Ф. Очок, К.А. Орлов та ін. // Промислова енергетика № 2, 2007

7. Очок В.Ф. Властивості теплоносіїв і робочих тел енергетики: інформація в Інтернеті / А.А. Александров, В.Ф. Очок, К.А. Орлов та ін. // Нове в російській електроенергетиці. №1, 2008

8. Alexandrov А.А.. , Ochkov VF, Orlov KA Steam Tables and Diagrams on Mathcad Calculation Server for Personal Computers, Pocket Computers and Smart Phones // Proceedings of the 15th International Conference of the Property of Water and Steam, Berlin / Germany, September 7-11, 2008

9. Очок В.Ф. Mathcad 14 для студентів і інженерів: російська офіційна версія. С-Пб .: БХВ-Петербург 2009

10. Очок В.Ф. Мережеві розрахунки і діаграми теплоенергетичних процесів // Промислова енергетика № 12, 2008

11. Очок В.Ф. Інтернет-розрахунки термодинамічних циклів / В.Ф. Очок, А.А. Александров, В.А. Волощук та ін. // Теплоенергетика, № 1 2009

12. Очок В.Ф. Фізичні та економічні величини в Mathcad і Maple. М .: Фінанси і статистика, 2002

13. Очок В.Ф., Янько А.Г. Математичні пакети і проблема передачі знань // Пленарна доповідь на VI школі-семінарі молодих вчених та спеціалістів академіка РАН В.Е.Алімасова «Проблеми тепломасообміну та гідродинаміки в енергомашинобудування», 16-18 вересня 2008 г. Казань, Росія

14. Теоретичні основи теплотехніки. Теплотехнічний експеримент: Довідник / Під загальною ред. А.В. Клименко і В.М. Зоріна. 3-е изд., Перераб. и доп. М .: Изд-во МЕІ, 2001.