Вимір е ня, операція, за допомогою якої визначається відношення однієї (вимірюваної) величини до іншої однорідної величини (що приймається за одиницю); число, що виражає таке відношення, називається чисельним значенням вимірюваної величини.

І. - одна з найдавніших операцій, що застосовувалася людиною в практичній діяльності (при розподілі земельних ділянок, в будівельній справі, при іригаційних роботах і т. Д.); сучасна господарсько-економічна і суспільне життя немислиме без І.

Для точних наук характерний органічний зв'язок спостережень і експерименту з визначенням чисельних значень характеристик досліджуваних об'єктів і процесів. Д. І. Менделєєв не раз підкреслював, що наука починається з тих пір, як починають вимірювати.

Закінчена І. включає наступні елементи: об'єкт І., властивість або стан якого характеризує вимірювана величина; одиницю І .; технічні засоби І., проградуйовані в вибраних одиницях; метод І .; спостерігача або реєструючий пристрій, що сприймає результат І .; остаточний результат І.

Найпростішим і історично першим відомим видом І. є пряме І., при якому результат виходить безпосередньо з І. самої величини (наприклад, І. довжини проградуірованной лінійкою, І. маси тіла за допомогою гир і т. Д.). Однак прямі І. не завжди можливі. У цих випадках вдаються до непрямих І., заснованим на відомій залежності між шуканої величиною і безпосередньо вимірюваними величинами.

Встановлені наукою зв'язки і кількісні відносини між різними за своєю природою фізичними явищами дозволили створити самоузгоджену систему одиниць, яка застосовується у всіх областях І. (див. Міжнародна система одиниць ).

І. слід відрізняти від інших прийомів кількісної характеристики величин, застосовуваних у тих випадках, коли немає однозначної відповідності між величиною і її кількісним вираженням в певних одиницях. Так, візуальне визначення швидкості вітру по Бофорта шкалою або твердості мінералів по Мооса шкалою слід вважати не І., а оцінкою .

Будь-яке І. неминуче пов'язано з погрішностями вимірів. Похибки, породжені недосконалістю методу І., неточної градуировкой і неправильною установкою вимірювальної апаратури, називають систематичними. Систематичні похибки виключають введенням поправок, знайдених експериментально. Похибки іншого типу - випадкові - обумовлені впливом на результат І. неконтрольованих чинників (ними можуть бути, наприклад, випадкові коливання температури, вібрації і т. Д.). Випадкові похибки оцінюються методами математичної статистики за даними багатократних І. (див. спостережень обробка ).

У деяких випадках - особливо часто зустрічаються в атомній і ядерній фізиці - розкид результатів І. пов'язаний не тільки з похибками апаратури, а й з характером самих досліджуваних явищ. Наприклад, якщо пучок однаково прискорених електронів пропустити через щілину дифракційних грат, то електрони з певною ймовірністю потраплять в різні точки поставленого за гратами екрану (див. дифракція часток ). Наведений приклад показує, що поширення І. на нові галузі фізики вимагає перегляду і уточнення понять, якими оперують при І. у інших областях. З розвитком науки і техніки виникла ще одна важлива проблема - автоматизація І. Це пов'язано, з одного боку, з умовами, в яких здійснюються сучасні І. (ядерні реактори, відкритий космос і т. Д.), З іншого боку - з недосконалістю органів почуттів людини. У сучасному виробництві, особливо в умовах високих швидкостей, тисків, температур, безпосереднє з'єднання вимірювальних пристроїв з регулюючими, минаючи людини, дозволяє перейти до найбільш досконалою формою виробництва - автоматизованого виробництва.

І. в метрології підрозділяються на прямі, непрямі, сукупні і спільні. Прямими називаються І., при яких міра або прилад застосовуються безпосередньо для І. даної величини (наприклад, І. маси на циферблатних або равноплечних вагах, І. температури термометром). Непрямими називаються І., результати яких знаходять на підставі відомої залежності між шуканої величиною і безпосередньо вимірюваними величинами (наприклад, І. щільності однорідного тіла по його масі і геометричним розмірам). Сукупними називаються І. декількох однойменних величин, значення яких знаходять вирішенням системи рівнянь, одержуваних в результаті прямих І. різних поєднань цих величин (наприклад, калібрування набору гирь, коли значення мас гирь знаходять на підставі прямого І. маси однієї з них і порівняння мас різних сполучень гир). Спільні І. - вироблювані одночасно І. двох або декількох різнойменних величин з метою знаходження залежності між ними (наприклад, знаходження залежності подовження тіла від температури).

Розрізняють також абсолютні і відносні І. До перших відносять непрямі І., засновані на І. одній або декількох основних величин (наприклад, довжини, маси, часу) і використанні значень фундаментальних фізичних постійних , Через які вимірювана фізична величина може бути виражена. Під другими розуміють І. або стосунки величини до однойменної величини, що грає роль довільної одиниці, або зміни величини відносно іншої, прийнятої за вихідну.

Знайдене в результаті І. значення вимірюваної величини є твір абстрактного числа (числового значення) на одиницю даної величини.

Результати І. через похибки завжди дещо відрізняються від істинного значення вимірюваної величини, тому результати І. зазвичай супроводжують вказівкою оцінки погрішності (див. похибки вимірювань ).

Забезпечення єдності І. в країні покладається на метрологічну службу, що зберігає еталони одиниць і що виробляє перевірку застосовуваних засобів І. Широкого поширення набула класифікація І. по об'єктах І. Відповідно до неї, розрізняють І. лінійні (І. довжини, площі, обсягу), механічні (І. сили, тиск і ін.), електричні і т. д. В Загалом ця класифікація відповідає основним розділам фізики.

Літ .: Маліков С. Ф., Тюрін Н. І., Введення в метрологію, 2 вид., М., 1966; Маліков С. Ф., Введення в техніку вимірювань, 2 вид., М., 1952; Яноші Л., Теорія і практика обробки результатів вимірів, пров. з англ., 2 вид., М., 1968; «Вимірювальна техніка», 1961, № 12: 1962 № 4, 6, 8, 9, 10.

К. П. Широков.

У математичної теорії І. відволікаються від обмеженої точності фізичних І. Завдання І. величини Q за допомогою одиниці міри U полягає в знаходженні числового множника q в рівності

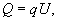(1)

при цьому Q і U вважаються позитивними скалярними величинами одного і того ж роду (див. величина ), А множник q - позитивне дійсне число, яке може бути як раціональним, так і ірраціональним. Для раціонального q = m / n (m і n - натуральні числа) рівність (1) має вельми простий сенс: воно означає, що існує така величина V (n -а частка від U), яка, будучи узята складовим n раз, дає U, будучи ж узята складовим m разів, дає Q:

.

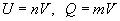В цьому випадку величини Q і U називаються сумірними. Для несумірних величин U і Q множник q ірраціональний (наприклад, дорівнює числу p, якщо Q є довжина кола, а U - її діаметр). У цьому випадку саме визначення сенсу рівності (1) дещо складніше. Можна визначити його так: рівність (1) позначає, що для будь-якого раціонального числа r

(2)

Досить зажадати, щоб умова (2) виконувалася для всіх десяткових наближень до q по недоліку і по надлишку. Слід зазначити, що історично саме поняття ірраціонального числа виникло із завдання І., так що первинне завдання в разі несумірних величин полягала власне не в тому, щоб визначити зміст рівності (1), виходячи з готової теорії дійсних чисел, а в тому, щоб встановити сенс символу q, що відображає результат порівняння величини Q з одиницею міри U. Наприклад, за визначенням німецького математика Р. Дедекинда, ірраціональне число є «перетин» в системі раціональних чисел. Такий перетин і з'являється природно при порівнянні двох несумірних величин Q і U. По відношенню до цих величин всі раціональні числа розділяються на два класи: клас R 1 раціональних чисел r, для яких Q> rU, і клас R 2 раціональних чисел r, для яких Q <rU.

Велике значення має наближене І. величин за допомогою раціональних чисел. Помилка наближеної рівності Q »rU дорівнює D = (r - qU). Природно шукати такі r = m / n, для яких помилка менше, ніж при будь-якому числі r '= m' / n 'з знаменником n' £ n. Такого роду наближення доставляються відповідними дробами r 1, r 2, r 3, ... до числа q, які знаходяться за допомогою теорії безперервних дробів . Наприклад, для довжини кола S, вимірюваної діаметром U, наближення такі:

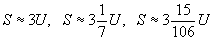
і т.д.; для довжини року Q, вимірюваною добою U, наближення такі:

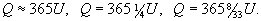
А. Н. Колмогоров.

І. в соціальному дослідженні (в статистиці, соціології, психології, економіці, етнографії), спосіб упорядкування соціальної інформації, при якому системи чисел і відносин між ними ставляться у відповідність ряду вимірюваних соціальних фактів. Різні заходи повторюваності, відтворюваності соціальних фактів і є соціальними вимірами, або шкалами. З розвитком суспільства набувають поширення прості шкали - грошова оцінка праці, розряди кваліфікації, оцінка успіхів у навчанні (система балів), спорті та ін. І. в суспільних науках відрізняється від таких «природних» шкал точним визначенням вимірюваних ознак і правил побудови шкали.

У соціальних дослідженнях І. вперше увійшли до вживання в 1920-30, коли дослідники зіткнулися з проблемою достовірності при вивченні суспільної свідомості, соціально-психологічних установок (відносин), соціального і професійного статусів, громадської думки, якісних характеристик умов праці і побуту і т. д. Ці І. є прикладом стандартизованої груповий оцінки, коли за допомогою методів вибіркової статистики вимірюється «інтенсивність» громадської думки.

І. поділяються на три типи: 1) номінальне - числа, що приписуються об'єктам на номінальній шкалі, лише констатують відміну або тотожність цих об'єктів, т. Е. Номінальна шкала є, по суті, угрупування або класифікація. 2) порядкове - числа, що приписуються об'єктам на шкалі, упорядковують їх по вимірюваній ознакою, але вказують лише на порядок розміщення об'єктів на шкалі, а не на відстань між об'єктами або, тим більше, координати; 3) інтервальний - числа, що приписуються об'єктам на шкалі, вказують не тільки на порядок об'єктів, але і на відстань між ними. Інтервальним І. є, наприклад, шкала привабливості професій. Така шкала, надаючи кожній професії умовний бал, дозволяє порівнювати професії по популярності, т. Е. Стверджувати, що, наприклад, професія шофера на М балів популярнішим професії слюсаря і на До балів менш популярна, ніж професія льотчика. Однак вона не дозволяє стверджувати, що інтерес до професій шофера і слюсаря перевищує інтерес до професії льотчика, якщо сума відповідних балів перевищує бал професії льотчика. Знаходження кількісної міри соціальних явищ і процесів обмежується цими трьома типами І. Робляться спроби створення четвертого типу І. - кількісного, з введенням одиниці І.

Літ .: Отрут В. А., Методологія і процедури соціологічних досліджень, Тарту, 1968; Здравомислов А. Г., Методологія і процедура соціологічних досліджень, М., 1969.

Ю. Б. Самсонов.