Опер а тори в квантової теорії, математичне поняття, широко використовується в математичному апараті квантової механіки і квантової теорії поля і служить для зіставлення певного вектору стану (або хвильової функції) y ін. певних векторів (функцій) y '. Співвідношення між y і y 'записується у вигляді y' = 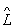y, де 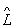- оператор. У квантовій механіці фізичним величинам (координаті, імпульсу, моменту кількості руху, енергії і т.д.) ставляться у відповідність О. 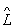(О. координати, О. імпульсу і т.д.), що діють на вектор стану (або хвильову функцію) y, т. Е. На величину, що описує стан фізичної системи.

Найпростіші види О., діючих на хвильову функцію y (х) (де х - координата частинки), - О. множення (наприклад, О. координати 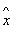, Y = х y) і о. диференціювання (наприклад, О. імпульсу 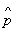, 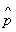y =, де i - уявна одиниця, 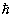- постійна Планка). Якщо y - вектор, компоненти якого можна представити у вигляді стовпчика чисел, то О. є квадратною таблицю - матрицю .

У квантовій механіці в основному використовуються лінійні оператори . Це означає, що вони мають наступну властивість: якщо 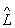y1 = y '1 і 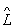y2 = y'2, то 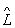(C 1 y1 + c 2 y2) = c 1 y'1 + c 2 y'2, де c 1 і з 2 комплексні числа. Це властивість відображає суперпозиції принцип -один з основних принципів квантової механіки.

Істотні властивості О. 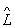визначаються рівнянням 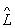y n = l n y n, де l n - число. Рішення цього рівняння y n називається власними функціями (власними векторами) оператора 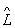. Власні хвильові функції (власні вектори стану) описують в квантовій механіці такі стани, в яких дана фізична величина L має певне значення l n. Числа l n називається власними значеннями О. 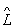, А їх сукупність - спектром О. Спектр може бути безперервним або дискретним; в першому випадку рівняння, що визначає y n, має рішення при будь-якому значенні l n (в певній галузі), у другому - рішення існують тільки при певних дискретних значеннях l n. Спектр О. може бути і змішаним: частково безперервним, частково дискретним. Наприклад, О. координати і імпульсу мають безперервний спектр, а О. енергії в залежності від характеру діючих в системі сил - безперервний, дискретний або змішаний спектр. Дискретні власні значення О. енергії називаються енергетичними рівнями.

Власні функції і власні значення О. фізичних величин повинні задовольняти певним вимогам. Т. к. Безпосередньо вимірювані физич. величини завжди приймають речовин. значення, то відповідні квантовомеханіч. О. повинні мати речовин. собств. значення. Далі, оскільки в результаті вимірювання физич. величини в будь-якому стані y мусить виходити одне з можливих власної. значень цієї величини, необхідно, щоб довільна хвильова функція (вектор стану) могла бути представлена ​​у вигляді лінійної комбінації власної. функцій (векторів) y n О. цієї физич. величини; ін. словами, сукупність власної. функцій (векторів) повинна становити повну систему. Цими властивостями володіють собств. функції і власної. значення т.зв. самосопряженних О., або ермітових операторів .

З О. можна виробляти алгебраїч. дії. Зокрема, під твором О. 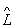1 і 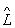2 розуміється такий О. 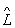= 1 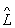2, дія якого на вектор (функцію) y дає 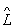y = y '', якщо 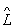2 y = y 'і 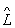1 y '= y' '.Проізведеніе О. в загальному випадку залежить від порядку співмножників, т. Е. 1 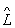2 ¹ 2 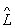1. Цим алгебра О. відрізняється від звичайної алгебри чисел. Можливість перестановки порядку співмножників в творі двох О. тісно пов'язана з можливістю одночасного вимірювання фізичних величин, яким відповідають ці О. 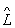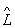Необхідною і достатньою умовою одночасної вимірності фізичних величин є рівність 1 2 = 2 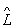1 (див. перестановки співвідношення ).

Рівняння квантової механіки можуть бути формально записані точно в тому ж вигляді, що і рівняння класичної механіки (гейзенбергівських подання до квантової механіки), якщо замінити фізичні величини, що входять в рівняння класичної механіки, відповідними їм О. Все відмінність між квантової і класичної механікою зведеться тоді до різниці алгебри. Тому О. в квантовій механіці іноді називають q -числами, на відміну від з -чісел, т. Е. Звичайних чисел, з якими має справу класична механіка.

О. можна не тільки множити, але і підносити до степеня, утворювати з них ряди і розглядати функції від О. Твір ермітових О. в загальному випадку не є ермітовим. У квантовій механіці використовуються і неермітови О., важливим класом яких є унітарні оператори . Унітарні О. не змінюють норм ( «довжин») векторів і «кутів» між ними. Незмінність норми вектора стану дає можливість інтерпретації його компонент як амплітуд імовірності рівним чином у вихідній і перетвореної функції. Тому дією унітарного О. описується розвиток квантово-механічної системи в часі, а також її зміщення в цілому в просторі, поворот, дзеркальне відображення і ін. Що Їх унітарними О. перетворення (унітарні перетворення) грають в квантовій механіці таку ж роль, яку в класичній механіці грають канонічні перетворення (див. Механіки рівняння канонічні ).

У квантовій механіці застосовується також О. комплексного сполучення, який не є лінійним. Твір такого О. на унітарний О. називаються антіунітарним О. Антіунітарние О. описують перетворення звернення часу і деякі ін.

В теорії квантових систем, що складаються з тотожних частинок, широко застосовується метод квантування вторинного , В якому розглядаються стану з невизначеним або змінним числом частинок і вводяться О., дія яких на вектор стану з даними числом частинок призводить до вектору стану зі зміненим на одиницю числом частинок (О. народження і поглинання часток). О. народження або поглинання частинки в даній точці х, (х) формально подібний хвильової функції y (х), як q- і с- числа, що відповідають одній і тій же фізичній величині відповідно в квантової і класичної механіки. Такі О. утворюють квантовані поля, які відіграють фундаментальну роль в релятивістських квантових теоріях (квантової електродинаміки, теорії елементарних частинок; см. Квантова теорія поля ).

Літ. см. при статтях Квантова механіка , Квантова теорія поля .

В. Б. Берестецький.