1. Чому штучне завищення в'язкості покращує збіжність задач обчислювальної гідродинаміки?
2. Реалізація методу штучного завищення в'язкості в COMSOL Multiphysics
3. Вибір параметра при налаштуванні параметричного дослідження
4. Ефективність методів завищення в'язкості і поступового підвищення нелінійності

Чи доводилося Вам моделювати турбулентні течії при вирішенні задач обчислювальної гідродинаміки? Тоді ви напевно знаєте, що виконання розрахунку іноді займає досить багато часу через складнощів, що виникають при пошуку чисельного рішення. Ці складності обумовлені нелінійністю рівнянь, що описують турбулентні потоки. Скоротити час розрахунку можна, якщо спочатку вирішити задачу з штучно завищеними значенням коефіцієнта в'язкості рідини, а потім використовувати отримане рішення в якості початкового наближення для задачі з більш низьким значенням в'язкості. Ми покажемо вам, як реалізувати цей підхід у середовищі COMSOL Multiphysics.

Чому штучне завищення в'язкості покращує збіжність задач обчислювальної гідродинаміки?

Перш ніж приступати до моделювання течії рідини, потрібно розрахувати число Рейнольдса, що характеризує цю течію. Число Рейнольдса за визначенням одно:

Re = \ frac {\ rho U d} {\ mu}

Тут \ rho - щільність середовища, що рухається, а \ mu - динамічний коефіцієнт в'язкості, U - характерна швидкість, d - характерний лінійний розмір системи.

Число Рейнольдса характеризує відношення сил інерції і в'язкості, що діють в потоці. Знаючи число Рейнольдса, можна визначити, який режим течії - ламінарний або турбулентний - ми повинні моделювати в COMSOL Multiphysics. Наприклад, в Мікроканали, де характерна швидкість і лінійний розмір відносно невеликі, значення число Рейнольдса мало, а значить режим течії ламінарний. Зворотний приклад - рух автомобіля з високою швидкістю. У цьому випадку перебіг характеризується високим значенням числа Рейнольдса, отже, режим течії турбулентний. В одній з попередніх статей блогу ми більш детально розповідали про визначення режиму течії.

Знайти чисельне рішення задачі про турбулентному плині, як правило, складніше, ніж в разі ламінарного потоку. Щоб зрозуміти, чому, давайте звернемося до рівнянь, що описують поле течії. У COMSOL Multiphysics турбулентні течії описуються осрдненнимі по Рейнольдсу рівняннями Нав'є-Стокса (RANS). У рівняння RANS вводиться нова змінна, що отримала назву турбулентної в'язкості, яка характеризує ступінь турбулентності потоку. Турбулентна в'язкість розраховується з використанням додаткових рівнянь, вид яких визначається використовуваної моделлю турбулентності.

Наприклад, для розрахунку турбулентної в'язкості в k-epsilon моделі турбулентності використовуються величини кінетичної енергії турбулентності (k) і турбулентної дисипації (epsilon). Рівняння моделі турбулентності за формою схожі на рівняння Нав'є-Стокса і теж містять лінійні і нелінійні члени. Нелінійність рівнянь турбулентності пояснює, чому при високих числах Рейнольдса набагато складніше домогтися збіжності завдання. Дізнатися, як вибрати модель турбулентності, ви можете з цієї статті в блозі .

Таким чином, для моделювання течій при великих числах Рейнольдса ми повинні використовувати моделі турбулентності, і рівняння, які вирішує COMSOL Multiphysics в цьому випадку, стають сильно нелінійними. Використання хороших початкових наближень може поліпшити збіжність нелінійних задач, як описано тут . Ступінь нелінійності рівнянь визначається в'язкістю рідини. Якщо спочатку задати в параметрах моделі високе значення коефіцієнта в'язкості, то тоді ми зможемо вирішити слабо нелінійну задачу, яка краще сходиться. Потім ми зможемо використовувати отримане рішення в якості гарного початкового наближення для рідини з більш низькою в'язкістю. Таким чином, ми підвищимо збіжність того завдання, яке хочемо вирішити. Цей підхід називається методом завищення в'язкості.

В рамках цього підходу завдання вирішується послідовно, при цьому спочатку в'язкість рідини штучно завищується, а потім поступово знижується, поки не досягне заданого значення. Рішення завдання, отримане при підвищеній в'язкості, використовується в якості початкового наближення для наступного кроку з меншою в'язкістю. Спочатку ми вирішуємо завдання з більш високою в'язкістю, знижуючи таким чином числом Рейнольдса. Тобто ми починаємо з рішення слабо нелінійної задачі, яка краще сходиться. Зменшуючи в'язкість (і тим самим збільшуючи число Рейнольдса) до заданого значення, ми переходимо від слабо нелінійної задачі до сильно нелінійної, і в кінці цієї процедури ми отримуємо рішення вихідної задачі. Давайте тепер подивимося, як цей підхід можна реалізувати в COMSOL Multiphysics.

Реалізація методу штучного завищення в'язкості в COMSOL Multiphysics

Давайте припустимо, що ви вже побудували CFD-модель в COMSOL Multiphysics і тепер хочете поліпшити її збіжність. Метод завищення в'язкості складається з трьох етапів.

• Завдання підвищує параметра
• Множення коефіцієнта в'язкості на підвищувальний параметр
• Налаштування параметричного дослідження

Спочатку потрібно поставити новий параметр, на який ми будемо множити коефіцієнт в'язкості. Значення, яке ми встановили для "visc_ramp" у вузлі Parameters байдуже, так як пізніше ми поставимо його через настройку параметричного дослідження (auxiliary sweep).

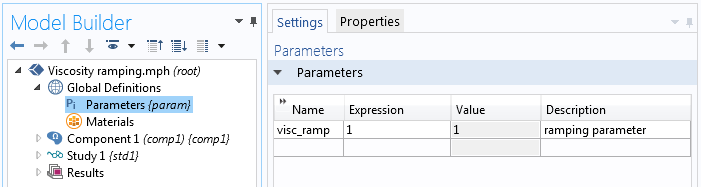
Задаємо параметр.

Потім перейдемо до вузла Materials і помножимо коефіцієнт в'язкості на параметр "visc_ramp". Наприклад, якщо "visc_ramp" має значення 100, розрахунок буде виконано для рідини, що має в 100 разів вищий коефіцієнт в'язкості, ніж задано за умовою задачі. В кінцевому підсумку, коли значення «visc_ramp» досягне 1, коефіцієнт в'язкості рідини повернеться до свого фактичним значенням.

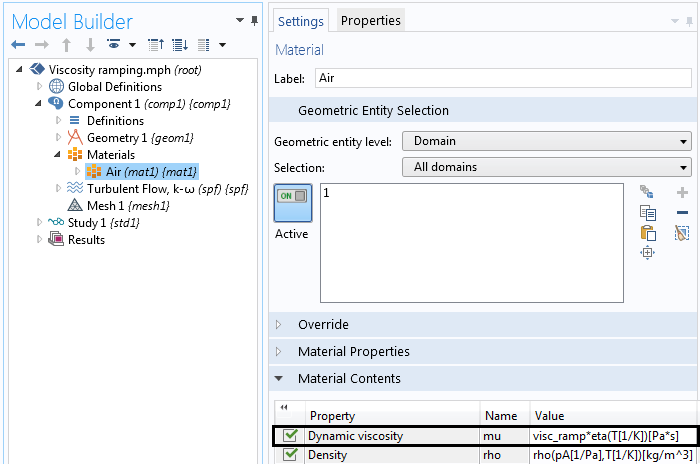
Множимо коефіцієнт в'язкості на параметр "visc_ramp".

В налаштуваннях стаціонарного решателя ми задаємо значення змінними параметрами "visc_ramp", дорівнює 1000, 100, 10 і 1. Після запуску параметричного дослідження спочатку буде розраховане рішення для першого значення параметра "visc_ramp" (1000), яке потім автоматично буде використано в якості початкового наближення для пошуку рішення при такому значенні параметра "visc_ramp" (100). Параметричне дослідження завершиться, коли параметр «visc_ramp» стане дорівнює 1, тобто коли буде знайдено рішення для фактичної в'язкості рідини.

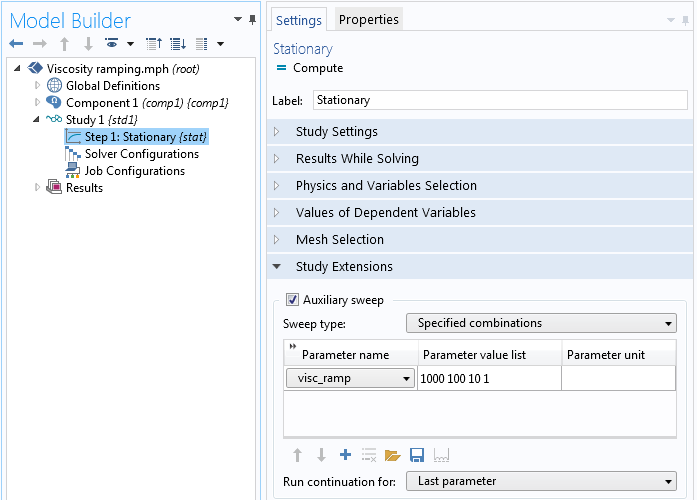
Налаштування стаціонарного решателя.

В процесі виконання розрахунку на вкладці Progress відображається поточне значення параметра "visc_ramp". В результаті збіжність досягнута, і ми можемо подивитися результати.

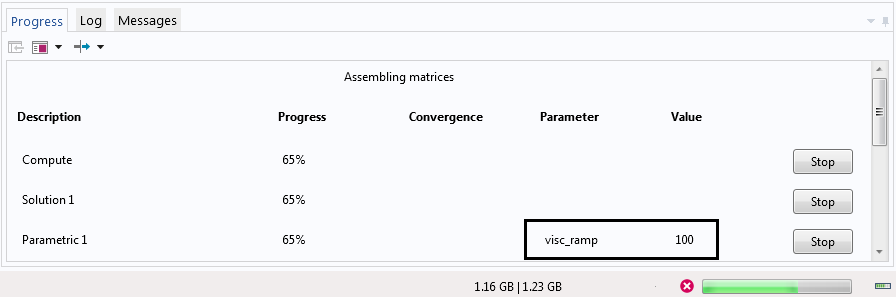
Вкладка Progress зі значенням параметра "visc_ramp", рівним 100.

Описана процедура штучного завищення в'язкості проілюстрована нижче. На малюнку показані лінії струму і поле швидкості турбулентного потоку за зворотним уступом, розраховані за допомогою моделі з Галереї додатків .

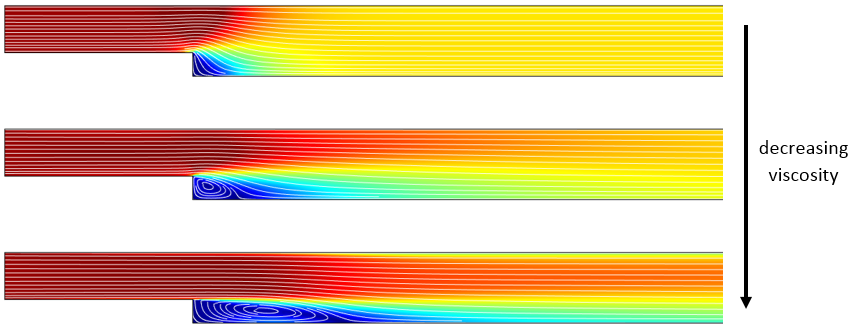
Лінії струму і поле швидкості при турбулентному плині в каналі зі зворотним уступом для трьох різних коефіцієнтів в'язкості.

Вибір параметра при налаштуванні параметричного дослідження

Найчастіше в якості початкового значення підвищує параметра для досягнення збіжності достатньо задати 100 або 10. Однак в тих випадках, коли домогтися збіжності важче, рекомендується використовувати більш високу початкове значення підвищує параметра, а потім знижувати його значення на порядок (наприклад, 1000, 100, 10, 1).

В даному випадку ми почали розрахунок поля течії для дуже в'язкої рідини (1000), визначили проміжні значення "visc_ramp" (100 і 10), щоб домогтися збіжності при фактичному значенні коефіцієнта в'язкості рідини ( "visc_ramp" = 1). Якщо не вдається знайти рішення при наступному нижчому значенні в'язкості, то автоматично буде зроблена спроба отримати рішення при значенні, що лежить між останнім що зійшов і наступним заданим користувачем значеннями параметра. Цей метод відомий як бектрекінг.

Щоб продемонструвати роботу бектрекінга, давайте запустимо параметричне дослідження, вибравши в якості значень "visc_ramp" 1000 і 1 Після того, як рішення для підвищувального параметра, дорівнює 1000, знайдено, програма спробує вирішити завдання при фактичному значенні в'язкості. Якщо вирішувач не вдається отримати сходяться рішення, тоді розрахунок повторюється для проміжного значення параметра (в даному випадку, 501). Коли рішення для параметра, рівного 501, отримано, програма знову спробує вирішити завдання при фактичному значенні в'язкості (параметр завищення в'язкості дорівнює 1), і, на цей раз розрахунок завершиться успішно!

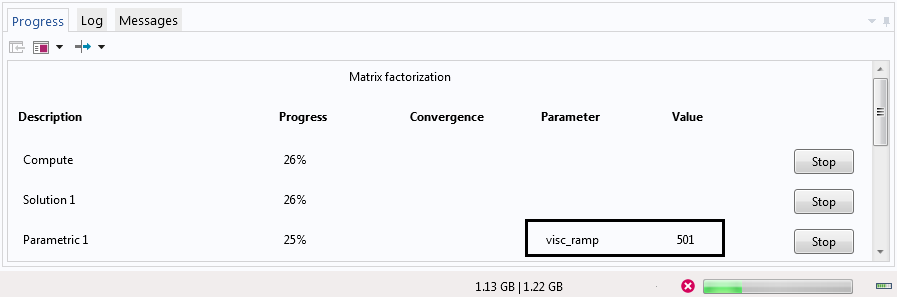
Вкладка Progress зі значенням параметра "visc_ramp", рівним 501.

Бектрекінг - це корисний вбудований алгоритм, який використовується вирішувачів для поліпшення збіжності при проведенні параметричних досліджень. Проте, користувач повинен вказати проміжні значення параметра, щоб забезпечити більш ефективний перехід Солвер від великих до менших значень.

Іноді, незважаючи на використання методу бектрекінга, рішення перестає сходиться при значенні параметра більше 1. Як правило, це означає, що для розрахунку поля течії використовується занадто груба сітка. В цьому випадку почати треба з побудови більш щільної сітки. Крім того, варто пам'ятати про необхідність дослідження завдання на чутливість до параметрів сітки . Такий аналіз є невід'ємною частиною верифікації отриманих результатів.

Ефективність методів завищення в'язкості і поступового підвищення нелінійності

Ми показали, як використовувати штучне завищення в'язкості в COMSOL Multiphysics для поліпшення збіжності задач обчислювальної гідродинаміки. Для цього ми налаштували параметричне дослідження, почавши рішення з завдання зі слабкою нелінійністю, а потім поступово підвищували ступінь нелінійності до тих пір, поки не отримали рішення вихідної задачі. Метод штучного завищення в'язкості досить корисний при вирішенні задач обчислювальної гідродинаміки, що характеризуються високими значеннями числа Рейнольдса, іншими словами, при моделюванні турбулентних течій.

Описаний спосіб зниження нелінійності може застосовуватися в самих різних завданнях. Наприклад, замість завищення в'язкості ми можемо поступово збільшувати силу тяжіння в задачах вільної конвекції або індекс плинності "n" при моделюванні течії неньютоновскіх рідин. Описана методика також може бути використана при вирішенні найширшого класу нелінійних мультіфізіческіх завдань, про що ми розповідаємо в цій публікації .

Для досягнення збіжності завдання ми можемо також використовувати метод поступового підвищення навантаження. Підвищення навантаження стосовно перебігу рідини, як правило, означає поступове збільшення швидкості на вході. Це ще один спосіб досягнення збіжності, про який не варто забувати.

Хочете дізнатися більше про ці методи і їх використанні при вирішенні ваших власних завдань в COMSOL Multiphysics? Будь ласка, Зв'яжіться з нами .