1. .Метод координат
2. ..Коллінеарние вектори
3. ..Компланарние вектори
4. ..Вектори в тривимірному геометричному просторі
5. ..Лінейная залежність векторів і розмірність простору

В. Г. Автор. Векторна і тензорна алгебра для майбутніх фізиків і техніків

суперобкладинка / Обкладинка / зміст

.Метод координат

Метод, який ми починаємо вивчати в цьому розділі, визначає найбільш сильну сторону векторної алгебри. Ось, що про це говорить Петро Костянтинович Рашевський:

"... велику і часто провідну роль в геометрії грає координатний метод. Тут геометричні образи вивчаються не безпосередньо геометрично, а методами алгебри (аналітична геометрія), а потім і аналізу (диференціальна геометрія). Величезна сила цього методу заснована на те, що він застосовує до геометрії сильний, добре розвинений обчислювальний апарат алгебри і аналізу. в результаті вдається ставити і вирішувати питання, лише мала частина яких укладається в порівняно вузькі рамки прямих геометричних методів "[13, с. 103].

..Коллінеарние вектори

Визначення (15)

Вектори називаються колінеарними, якщо вони паралельні.

Якби ми завжди мали справу з геометричними векторами, то нове слово "Колінеарні" було б зайвим. Поняття про паралельних об'єктах занадто сильно пов'язано з нашими геометричними уявленнями. Однак в математиці слово "вектор" має ширше значення, і застосовується для таких векторів, про які ми не можемо сказати, що вони паралельні.

Оскільки вектори, які можуть бути суміщені за допомогою паралельного перенесення, вважаються рівними, можна Колінеарні вектори розглядати як лежать на одній прямій.

Будь-які два вектори, що лежать на одній прямій, можуть відрізнятися довжинами і можуть мати або однакові, або протилежні напрямки. Тому для будь-яких двох колінеарних векторів 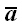і справедливо співвідношення: 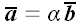, де 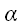- дійсне число.

Визначення (16)

Якщо один з векторів, що не рівний нулю, ми приймемо за міру і позначимо його , То всі інші вектори можуть бути представлені в однаковій формі 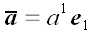. вектор називається при цьому базисним вектором, а 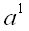- координатою вектора 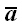щодо даного базису. Вектори базису можна писати без "векторної" риси зверху. Неважко бачити, що 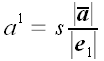. Можна також написати, що .

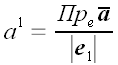Звичайно, для колінеарних векторів всі ці визначення і позначення є зайвими, і ми ввели їх для того, щоб використовувати в більш складних і цікавих випадках.

..Компланарние вектори

Визначення (17)

Вектори називаються компланарними, якщо вони паралельні деякій площині.

Оскільки вільні вектори можна переносити паралельно самим собі в просторі, то можна вважати, що всі компланарні вектори лежать в одній площині.

Будь-вектор, паралельний прямій, можна висловити через базисний вектор на цій прямій 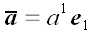, Але якщо вектор 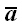на цій прямій не лежить, то цього зробити вже не можна. Однак, якщо ми виберемо на площині два базисних вектора і 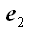, То будь-який інший вектор вже може бути виражений у вигляді лінійної комбінації базисних векторів 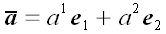. При цьому вектори і 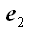називаються базисом, а числа 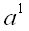і 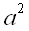координатами вектора 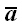в цьому базисі.

Справді, спроектуємо вектор 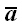на пряму, збігається з вектором , У напрямку вектора 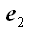і на пряму, збігається з вектором 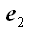, У напрямку вектора (Рис. 12).

Мал. 12

Очевидно, що 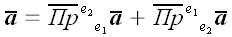. Оскільки кожну проекцію в свою чергу можна виразити через базисний вектор, то 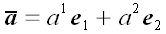. де,

, .

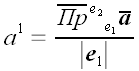(3)

..Вектори в тривимірному геометричному просторі

Два вектора завжди є компланарними так само, як три точки завжди лежать в одній площині. Але три вектора вже можуть не бути компланарними, і тоді будь-який з них не може бути виражений через два інших. Але, якщо ми виберемо в просторі три некомпланарних базисних вектора, то будь-який четвертий вже може бути виражений через них у вигляді лінійної комбінації.

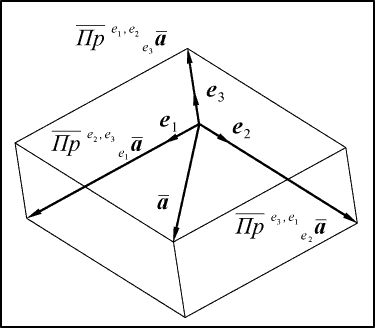
Мал. 13

Поступаючи аналогічно тому, як ми це зробили для "плоского" випадку, спроектуємо вектор 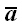на базисні вектори , 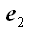і за допомогою проектують площин ( 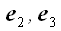), ( ) 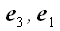І ( 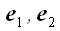) (Рис. 13). Висловивши кожну з проекцій через відповідний вектор базису, отримаємо:

.

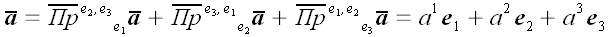Те ж саме в скороченою записи:

.

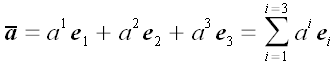Угода Ейнштейна про позначеннях

Оскільки в векторній алгебрі подібного роду суми зустрічаються часто, то за пропозицією А. Ейнштейна прийнято знак суми опускати. З урахуванням угоди А. Ейнштейна, остання рівність можна переписати в більш компактному вигляді: .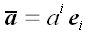

Ось і все, треба тільки не забувати, що останній запис є всього лише скороченням попередньої. Символ i в останньому виразі можна замінити будь-яким іншим, і від цього нічого не зміниться, тому його називають німим символом. Німий символ пробігає всі можливі значення. У нашому випадку - це 1, 2, 3. Цікаво, що останній вираз в скороченою записи А. Ейнштейна виглядає зовсім однаково для всіх трьох випадків, які ми розглянули, якщо врахувати, що для векторів на площині i приймає значення 1 і 2, а для векторів на прямій єдине значення - 1.

Уточнимо поняття базису. Перш за все, базові вектори - це такі вектори, через які можуть бути однозначно виражені інші. Але таких векторів багато, і, коли ми говоримо про вектори базису, передбачається, що якісь вектори для цієї мети ми вже вибрали. У тривимірному просторі ми можемо вибрати в якості базису будь-які три некомпланарних вектора.

..Лінейная залежність векторів і розмірність простору

Визначення (19)

вектори 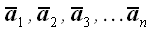називаються лінійно залежними, якщо можна підібрати не всі рівні нулю числа 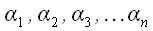, Такі що виконується рівність: .

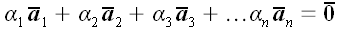З іншого боку, якщо таких чисел не існує, то вектори називаються лінійно незалежними.

1. Три вектори лінійно залежні тоді і тільки тоді, коли вони компланарні.

Справді, нехай вектори 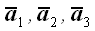лінійно залежні. тоді 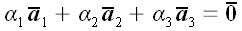, І серед чисел 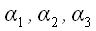є нерівні нулю. Нехай, для визначеності, не дорівнює нулю перше число 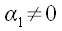. У цьому випадку ми маємо право записати: 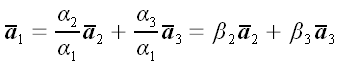. Але це означає, що вектори 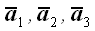лежать в одній площині, якщо, звичайно, їх перенести до одного початку. Отже, вектори 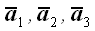компланарність.

З іншого боку, якщо вектори 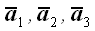компланарність, то можна вважати, що вони лежать в одній площині. Тут можливі варіанти, які ми розглянемо окремо.

Варіант 1.

Один з векторів 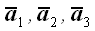є нульовим вектором. Нехай, для визначеності, це буде перший вектор. У цьому випадку ми можемо записати: .

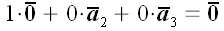Варіант 2.

серед векторів 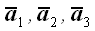немає нульових векторів, але є Колінеарні. Нехай, для визначеності, колінеарними є перші два вектора. Але в цьому випадку, перший вектор може бути виражений через другий: , і, отже, .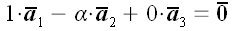

Варіант 3.

серед векторів 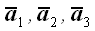немає нульових векторів, і всі вектори не є попарно колінеарними. В цьому випадку всі вектори можуть бути перенесені в одну площину, і будь-який з них може бути розкладений по іншим як по векторах базису. отже, 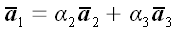, І ми знову отримуємо, що: .

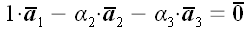2. Будь-які чотири вектори в тривимірному просторі завжди лінійно залежні.

Тут також можливі два варіанти.

Варіант 1.

Будь-які три вектори є компланарними. Нехай, для визначеності, цими векторами будуть перші три. У цьому випадку ми можемо підібрати не всі рівні нулю числа 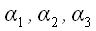так що 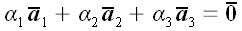. Але тоді

Варіант 2.

Будь-які три вектори не є компланарними. У цьому випадку будь-який з чотирьох векторів може бути розкладений по іншим трьом як по базису 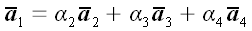, І ми можемо записати, що .

Отже, в обох можливих випадках чотири вектора є лінійно залежними.

Резюмую всі ці результати, можна сказати, що в тривимірному просторі ми завжди можемо вибрати три лінійно незалежних вектора. У той же час, будь-які чотири вектори є лінійно залежними.

Ми також показали, що в площині будь-які три вектори є лінійно залежними, в той же час в площині завжди можна знайти два лінійно незалежних вектора, так як для цього достатньо, щоб вони не були колінеарні.

Це дає нам підставу дати наступне визначення розмірності простору векторів.

Визначення розмірності простору (20)

Найбільше число лінійно незалежних векторів простору називається його розмірністю.

Розмірність простору збігається з числом базисних векторів цього простору. Оскільки будь-який вектор може бути розкладений за векторами базису, ми можемо дати наступне визначення координат вектора в довільному базисі.

Визначення координат вектора (21)

коефіцієнти 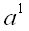, , 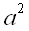, ... 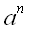в розкладанні вектора 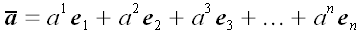по базису , , 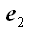... 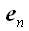називаються координатами вектора 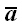в цьому базисі.

Визначення, наведені в цьому розділі, хороші тим, що вони легко узагальнюються на простору будь-яких розмірностей. Але навіщо це потрібно? Адже ми прекрасно знаємо, що наше звичне і затишний простір трехмерно. Можна ще говорити про двовимірному просторі векторів на площині або про одновимірному - на прямій. Але оскільки більше трьох не буває, чи варто городити весь цей город?

Що являє собою, наприклад, чотиривимірний простір? На це питання будь-фізик-теоретик скаже, що наш простір тільки наближено можна вважати тривимірним. Простір не існує поза часом, а разом з часом воно утворює чотиривимірний простір-час. У більш "просунутих" теоріях вже неможливо обійтися без одинадцяти-мірних просторів. Але навіть якщо всі ці теоретичні абстракції душа не приймає, і ми ні за що не хочемо залишати звичного тривимірного простору, нам все одно не уникнути уявлення про багатовимірних просторах. Ну, добре, наш простір трехмерно, але чому воно трехмерно? Вже сама постановка цього питання передбачає необхідність говорити і міркувати про просторах з великим числом вимірів.

Є й більш прагматичні причини для інтересу до багатовимірним просторів. Наприклад, вектор-стовпці і вектор-рядки - типові об'єкти матричної алгебри - є векторами в сенсі нашого спільного визначення вектора (8).

Нехай, скажімо,

, , , , .

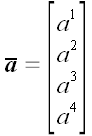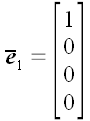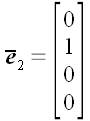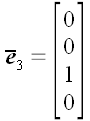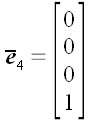З цими формальними векторами ми можемо звертатися, як зі звичайними векторами, наприклад, розкласти вектор 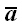по базису , , , :

.

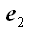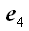Такого роду формальні структури з необхідністю виникають в різних областях знання і дуже приємно, що не потрібно щоразу будувати заново всю теорію.