1. Поняття алгебраїчної лінії і її порядку
2. Що таке канонічний вид рівняння?
3. Класифікація ліній другого порядку
4. Еліпс і його канонічне рівняння
5. Як побудувати еліпс?
6. Визначення еліпса. Фокуси еліпса і ексцентриситет еліпса
7. Як знайти фокуси еліпса?
8. Ексцентриситет еліпса і його геометричний сенс
9. Окружність - це окремий випадок еліпса
10. Поворот і паралельне перенесення еліпса

Після ґрунтовного опрацювання прямих на площині продовжуємо вивчати геометрію двовимірного світу. Ставки подвоюються, і я запрошую вас відвідати мальовничу галерею еліпсів, гіпербол, парабол, які є типовими представниками ліній другого порядку. Екскурсія вже почалася, і спочатку коротка інформація про всю експозиції на різних поверхах музею:

Поняття алгебраїчної лінії і її порядку

Лінію на площині називають алгебраїчною, якщо в аффинной системі координат її рівняння має вигляд 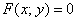, де 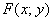- многочлен, що складається з доданків виду 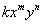( 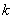- дійсне число, 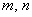- цілі невід'ємні числа).

Як бачите, рівняння алгебри лінії не містить синусів, косинусів, логарифмів і іншого функціонального бомонду. Тільки «ікси» і «ігреки» в цілих невід'ємних ступенях.

Далі під словом «лінія» за замовчуванням буде матися на увазі алгебраїчна лінія на площині

Порядок лінії дорівнює максимальному значенню 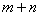що входять в нього доданків.

За відповідної теореми, поняття алгебраїчної лінії, а також її порядок не залежать від вибору аффинной системи координат , Тому для легкості буття вважаємо, що всі наступні викладки мають місце бути в декартових координатах .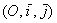

Загальне рівняння лінії другого порядку має вигляд 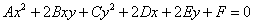, де 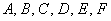- довільні дійсні числа ( 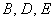прийнято записувати з множітелем- «двійкою»), причому коефіцієнти 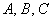нерівні одночасно нулю.

якщо 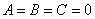, То рівняння спрощується до 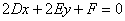, І якщо коефіцієнти 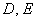одночасно не рівні нулю, то це в точності загальне рівняння «плоскою» прямий , Яка представляє собою лінію першого порядку.

Багато хто зрозумів сенс нових термінів, але, тим не менш, з метою 100% -го засвоєння матеріалу сунемо пальці в розетку. Щоб визначити порядок лінії, потрібно перебрати всі складові її рівняння і у кожного з них знайти суму ступенів входять змінних.

наприклад:

доданок 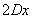містить «ікс» в 1-го ступеня;
доданок 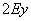містить «ігрек» в 1-го ступеня;
в слагаемом 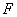змінні відсутні, тому сума їх ступенів дорівнює нулю.

Далі з отриманих чисел вибирається максимальне значення, в даному випадку одиниця, - це і є порядок лінії.

Тепер розберемося, чому рівняння 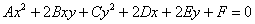задає лінію другого порядку:

доданок 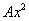містить «ікс» у 2-го ступеня;
у доданка 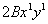сума ступенів змінних: 1 + 1 = 2;
доданок 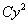містить «ігрек» у 2-го ступеня;
всі інші складові - меншою мірою.

Максимальне значення: 2

Якщо до нашого рівняння додатково приплюсувати, скажімо, 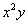, То воно вже буде визначати лінію третього порядку. Очевидно, що загальний вид рівняння лінії 3-го порядку містить «повний комплект» доданків, сума ступенів змінних в яких дорівнює трьом:
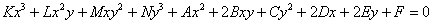, Де коефіцієнти 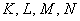нерівні одночасно нулю.

У тому випадку, якщо додати одне або декілька відповідних доданків, які містять 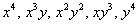, То мова вже зайде про лінії 4-го порядку, і т.д.

З алгебраїчними лініями 3-го, 4-го і більш високих порядків нам доведеться зіткнутися ще не раз, зокрема, при знайомстві з полярної системою координат .

Однак повернемося до загального рівняння 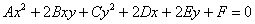і згадаємо його найпростіші шкільні варіації. Як приклади напрошується парабола 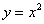, Рівняння якої легко привести до загального вигляду 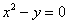, І гіпербола 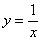з еквівалентним рівнянням 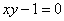. Однак не все так гладко ....

Істотний недолік загального рівняння полягає в тому, що в більшості випадків не зрозуміло, яку лінію воно задає. Навіть в найпростішому випадку 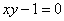не відразу збагнеш, що це гіпербола. Такі розклади гарні тільки на маскараді, тому в курсі аналітичної геометрії розглядається типова задача приведення рівняння лінії 2-го порядку до канонічного вигляду .

Що таке канонічний вид рівняння?

Це загальноприйнятий стандартний вид рівняння, коли в лічені секунди стає ясно, який геометричний об'єкт воно визначає. Крім того, канонічний вид дуже зручний для вирішення багатьох практичних завдань. Так, наприклад, з канонічного рівняння 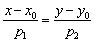«Плоскою» прямий , По-перше, відразу зрозуміло, що це пряма, а по-друге - елементарно проглядається належить їй точка 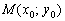і спрямовує вектор .

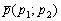Очевидно, що будь-яка лінія 1-го порядку представляє собою пряму. На другому ж поверсі нас чекає вже не вахтер, а набагато більш різноманітна компанія з дев'яти статуй:

Класифікація ліній другого порядку

За допомогою спеціального комплексу дій будь-яке рівняння лінії другого порядку приводиться до одного з наступних видів:

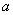( і 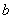- позитивні дійсні числа)

1) 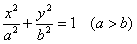- канонічне рівняння еліпса;

2) 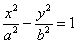- канонічне рівняння гіперболи;

3) 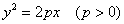- канонічне рівняння параболи;

4) 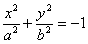- уявний еліпс;

5) 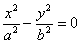- пара пересічних прямих;

6) 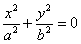- пара уявних пересічних прямих (з єдиною дійсною точкою перетину на початку координат);

7) 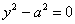- пара паралельних прямих;

8) 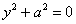- пара уявних паралельних прямих;

9) 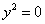- пара збіглися прямих.

У ряду читачів може скластися враження неповноти списку. Наприклад, в пункті № 7 рівняння 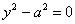задає пару прямих 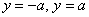, Паралельних осі 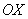, І виникає питання: а де ж рівняння 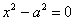, Що визначає прямі 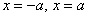, Паралельні осі ординат? Відповідь: воно не вважається канонічним. прямі 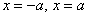являють собою той же самий стандартний випадок 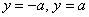, Повернений на 90 градусів, і додаткова запис 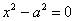в класифікації надлишкова, оскільки не несе нічого принципово нового.

Таким чином, існує дев'ять і тільки дев'ять різних видів ліній 2-го порядку, але на практиці найбільш часто зустрічаються еліпс, гіпербола і парабола .

Спочатку розглянемо еліпс. Як завжди, я акцентую увагу на тих моментах, які мають велике значення для вирішення завдань, і якщо вам необхідний детальний висновок формул, доведення теорем, будь ласка, зверніться, наприклад, до підручника Базильова / Атанасян або Александрова.

Еліпс і його канонічне рівняння

Правопис ... будь ласка, не повторюйте помилок деяких користувачів Яндекса, яких цікавить «як побудувати еллібз», «відмінність еліпса від овалу» і «ексцентриситет елебса».

Канонічне рівняння еліпса має вигляд 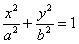, де 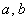- позитивні дійсні числа, причому 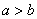. Саме визначення еліпса я сформулюю пізніше, а поки самий час відпочити від говорильні і вирішити поширену задачу:

Як побудувати еліпс?

Так, ось взяти його і просто накреслити. Завдання зустрічається часто, і значна частина студентів не зовсім грамотно справляються з кресленням:

приклад 1

Побудувати еліпс, заданий рівнянням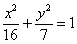

Рішення: спочатку наведемо рівняння до канонічного виду: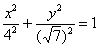

Навіщо приводити? Одна з переваг канонічного рівняння 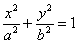полягає в тому, що воно дозволяє моментально визначити вершини еліпса, які знаходяться в точках 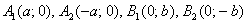. Легко помітити, що координати кожної з цих точок задовольняють рівняння .

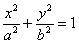В даному випадку :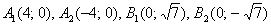

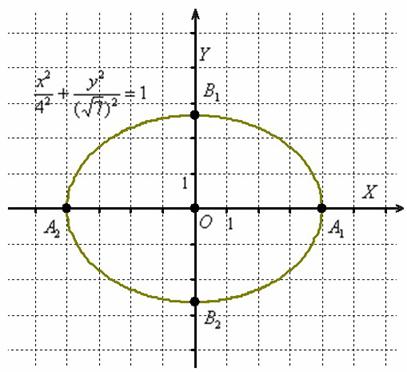
відрізок 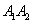називають великою віссю еліпса;
відрізок 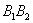- малої віссю;
число 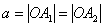називають велика піввісь еліпса;
число 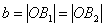- малої полуосью.
в нашому прикладі: .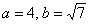

Щоб швидко уявити, як виглядає той чи інший еліпс досить подивитися на значення «а» і «бе» його канонічного рівняння.

Все гаразд, складно і красиво, але є один нюанс: я виконав креслення за допомогою програми . І ви можете виконати креслення за допомогою будь-якої програми. Однак в сувору дійсність на столі лежить картатий листок паперу, і на наших руках водять хороводи миші. Люди з художнім талантом, звичайно, можуть посперечатися, але миші є і у вас теж (правда, трохи менше). Таки недарма людство винайшло лінійку, циркуль, транспортир і інші нехитрі пристосування для креслення.

З цієї причини нам навряд чи вдасться акуратно накреслити еліпс, знаючи одні вершини. Ще так-сяк, якщо еліпс невеликий, наприклад, з півосями 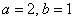. Як варіант, можна зменшити масштаб і, відповідно, розміри креслення. Але в загальному випадку вкрай бажано знайти додаткові точки.

Існує два підходи до побудови еліпса - геометричний і алгебраїчний. Побудова за допомогою циркуля і лінійки мені не подобається через не самого короткого алгоритму і суттєвою захаращеності креслення. У разі крайньої необхідності, будь ласка, зверніться до підручника, а в реальності ж набагато раціональніше скористатися засобами алгебри. З рівняння еліпса 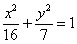на чернетці швиденько висловлюємо: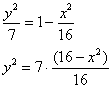

Далі рівняння розпадається на дві функції: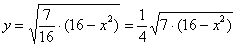
- визначає верхню дугу еліпса;
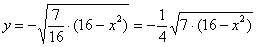- визначає нижню дугу еліпса.

Заданий канонічним рівнянням еліпс симетричний щодо координатних осей, а також щодо початку координат. І це чудово - симетрія майже завжди провісник халяви. Очевидно, що досить розібратися з 1-й координатної чвертю, тому нам буде потрібно функція 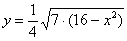. Напрошується знаходження додаткових точок з абсциссами 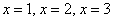. Настукаем три смс-ки на калькуляторі: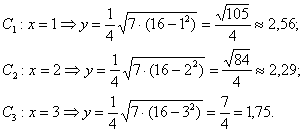

Безумовно, приємно і те, що якщо допущена серйозна помилка в обчисленнях, то це відразу з'ясується в ході побудови.

Відзначимо на кресленні точки 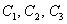(Червоний колір), симетричні точки на інших дугах (синій колір) і акуратно з'єднаємо лінією всю компанію: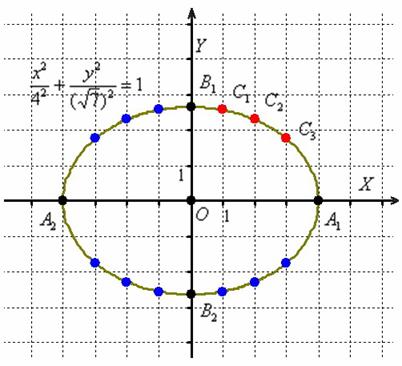

Первинний нарис краще прокреслити тонко-тонко, і тільки потім додати натиск олівця. В результаті має вийти цілком гідний еліпс. До речі, чи не бажаєте дізнатися, що це за крива?

Визначення еліпса. Фокуси еліпса і ексцентриситет еліпса

Еліпс - це окремий випадок овалу. Слово «овал» не слід розуміти в обивательському розумінні ( «дитина намалював овал» і т.п.). Це математичний термін, що має розгорнуту формулювання. Метою даного уроку не є розгляд теорії овалів і різних їх видів, яким практично не приділяється уваги в стандартному курсі аналітичної геометрії. І, відповідно до більш актуальними потребами, ми відразу переходимо до суворому визначенню еліпса:

Еліпс - це безліч всіх точок площині, сума відстаней до кожної з яких від двох даних точок 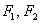, Званих фокусами еліпса, - є величина постійна, чисельно рівна довжині великої осі цього еліпса: .
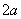При цьому відстані між фокусами менше даного значення: .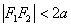

Зараз стане все зрозуміліше: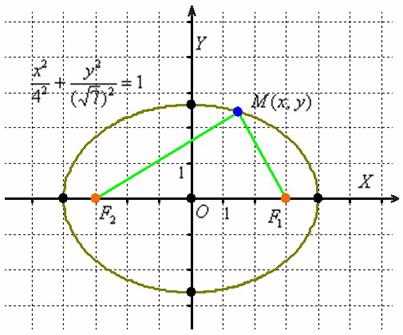

Уявіть, що синя точка «їздить» по еліпсу. Так ось, яку б точку еліпса 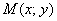ми не взяли, сума довжин відрізків 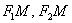завжди буде однією і тією ж: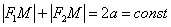

Переконаємося, що в нашому прикладі значення суми 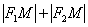дійсно дорівнює восьми. Подумки помістіть точку «ем» в праву вершину еліпса, тоді: 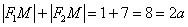, Що і було потрібно перевірити.

На визначенні еліпса заснований ще один спосіб його креслення. Вища математика, часом, причина напруги і стресу, тому саме час провести черговий сеанс розвантаження. Будь ласка, візьміть ватман або великий аркуш картону і приколоти його до столу двома гвоздиками. Це будуть фокуси 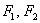. До стирчить капелюшках цвяхів прив'яжіть зелену нитку і до упору відтягніть її олівцем. Гриф олівця виявиться в деякій точці 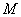, Яка належить еліпсу. Тепер починайте вести олівець по аркушу паперу, зберігаючи зелену нитку сильно натягнутої. Продовжуйте процес до тих пір, поки не повернетеся у вихідну точку ... відмінно ... креслення можна здати на перевірку лікаря викладачеві =)

Як знайти фокуси еліпса?

У наведеному прикладі я зобразив «готовенькі» точки фокусу, і зараз ми навчимося добувати їх з надр геометрії.

Якщо еліпс заданий канонічним рівнянням 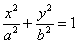, То його фокуси мають координати 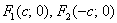, де 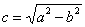- це відстань від кожного з фокусів до центру симетрії еліпса.

Обчислення простіше простого: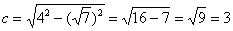

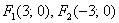
! Зі значенням «це» не можна ототожнювати конкретні координати фокусів! Повторюся, що 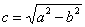- це ВІДСТАНЬ від кожного з фокусів до центру (який в загальному випадку не зобов'язаний розташовуватися саме на початку координат).
І, отже, відстань між фокусами 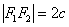теж не можна прив'язувати до канонічного положення еліпса. Іншими словами, еліпс можна перенести в інше місце і значення 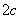залишиться незмінним, в той час як фокуси, природно, поміняють свої координати. Будь ласка, враховуйте даний момент в ході подальшого вивчення теми.

Їдемо далі:

Ексцентриситет еліпса і його геометричний сенс

Ексцентриситетом еліпса називають відношення 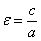, Яке може набувати значень в межах .

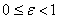У нашому випадку: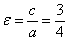

З'ясуємо, як форма еліпса залежить від його ексцентриситету. Для цього зафіксуємо ліву і праву вершини розглянутого еліпса, тобто, значення великої півосі 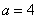залишатиметься постійним. Тоді формула ексцентриситету набуде вигляду: .

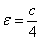Почнемо наближати значення ексцентриситету до одиниці. Це можливо тільки в тому випадку, якщо 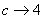. Що це означає? ... згадуємо про фокуси 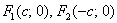. Це означає, що фокуси еліпса будуть «роз'їжджатися» по осі абсцис до бічних вершин. І, оскільки «зелені відрізки не гумові», то еліпс неминуче почне сплющуватися, перетворюючись все в більш і більш тонку сосиску, нанизану на вісь .

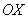Таким чином, чим ближче значення ексцентриситету еліпса до одиниці, тим еліпс більш довгасті.

Тепер змоделюємо протилежний процес: фокуси еліпса 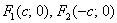пішли назустріч один одному, наближаючись до центру. Це означає, що значення «це» стає все менше і, відповідно, ексцентриситет прагне до нуля: .
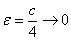При цьому «зеленим відрізках» буде, навпаки - «ставати тісно» і вони почнуть «виштовхувати» лінію еліпса вгору і вниз.

Таким чином, чим ближче значення ексцентриситету до нуля, тим еліпс більше схожий на ... дивимося граничний випадок 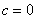, Коли фокуси успішно возз'єдналися на початку координат:

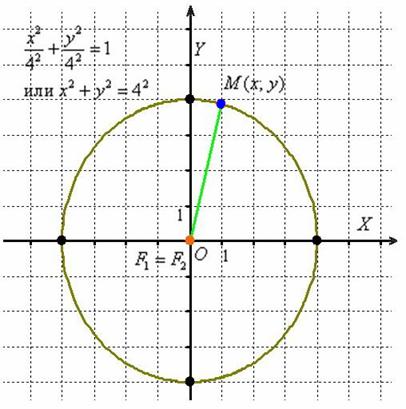
Окружність - це окремий випадок еліпса

Дійсно, в разі рівності піввісь канонічне рівняння еліпса 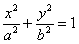набирає вигляду 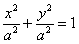, Який рефлекторно перетвориться до 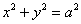- добре відомому зі школи рівняння кола з центром на початку координат радіуса «а».

На практиці частіше використовують запис з «говорить» буквою «ер»: 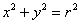. Радіусом називають довжину відрізка 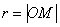, При цьому кожна точка 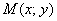кола віддалена від центру 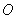на відстань радіуса.

Зауважте, що визначення еліпса залишається повністю коректним: фокуси збіглися 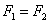, І сума довжин збіглися відрізків 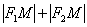для кожної точки окружності - є величина постійна. Так як відстань між фокусами 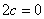, То ексцентриситет 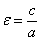будь-кола дорівнює нулю.

Будується коло легко і швидко, досить озброїтися циркулем. Проте, іноді буває потрібно з'ясувати координати деяких її точок, в цьому випадку йдемо знайомим шляхом - наводимо рівняння 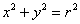до бадьорого матановскому увазі: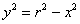

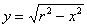- функція верхньої півкола;
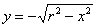- функція нижньої півкола.

Після чого знаходимо потрібні значення, диференціюючи , інтегруємо і робимо інші хороші речі.

Стаття, звичайно, носить довідковий характер, але як на світі без любові прожити? Творче завдання для самостійного рішення

приклад 2

Скласти канонічне рівняння еліпса, якщо відомий один з його фокусів 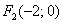і мала піввісь 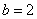(Центр знаходиться на початку координат). Знайти вершини, додаткові точки і зобразити лінію на кресленні. Обчислити ексцентриситет.

Рішення і креслення в кінці уроку

Додамо екшену:

Поворот і паралельне перенесення еліпса

Повернемося до канонічного рівняння еліпса 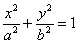, А саме, до умови 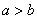, Загадка якого терзає допитливі ще з часів першої згадки про даної кривої. Ось ми розглянули еліпс 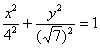, Але хіба на практиці не може зустрітися рівняння 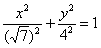? адже тут 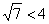, Однак, це начебто як теж еліпс!

Подібне рівняння нечасто, але дійсно трапляється. І воно дійсно визначає еліпс. Розвіємо містику: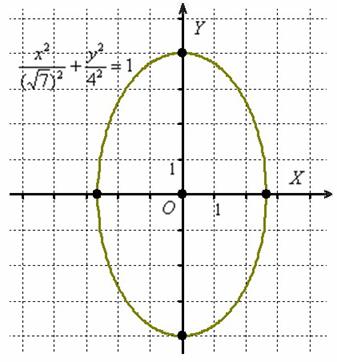

В результаті побудови отриманий наш рідний еліпс, повернений на 90 градусів. Тобто, 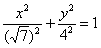- це неканонічна запис еліпса 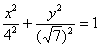. Запис! - рівняння 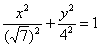НЕ задає якийсь інший еліпс, оскільки на осі 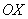не існує точок 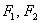(Фокусів), які б задовольняли визначенням еліпса.

Як бути, якщо таке диво-яйце все-таки трапилося на життєвому шляху? У тому випадку якщо вам запропоновано побудувати еліпс, то, напевно, краще побудувати його в нестандартному вигляді. З вершинами і додатковими точками, думаю, проблем не виникне. Але якщо вам запропоновано знайти фокуси, ексцентриситет і т.д., то настійно рекомендую почати (або продовжити після креслення) рішення так:

«Повернемо еліпс на 90 градусів і перепишемо його рівняння 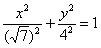в канонічному вигляді: 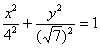»- далі за звичайною схемою.

! Примітка: в теорії прийнято повертати не саму фігуру, а осі! І якщо від вас ПОТРІБНО привести рівняння до канонічного виду , То рішення, строго кажучи, слід оформити інакше: «Перейдемо до нової прямокутної системі координат 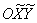, Повернувши координатні осі на 90 градусів проти годинникової стрілки, і запишемо рівняння еліпса в канонічному вигляді: ».

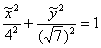Втім, ерудити можуть встати на слизьку доріжку плутанини, модифікувавши всі розрахунки з урахуванням повороту. Але все одно не раджу. Тому що по-дитячому. Адже еліпс можна повернути і на інший кут =) Про це ми ще поговоримо пізніше.

У практичних завданнях набагато частіше зустрічається паралельний перенос еліпса:

рівняння 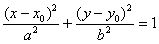задає еліпс з велика піввісь «а», малої полуосью «бе» і центром симетрії в точці .

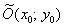Зобразимо на кресленні еліпс 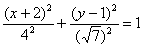. Відповідно до формули: 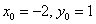, Тобто наш піддослідний еліпс «переїхав» у точку :

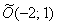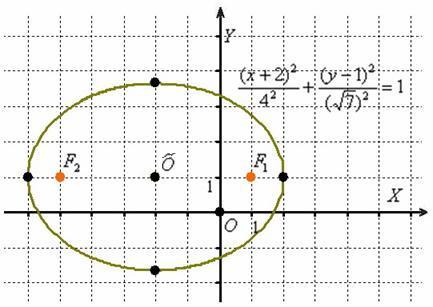
значення 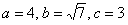залишилися колишніми, а ось фокуси, зрозуміло, мігрували, і формули їх координат доведеться знаходити з поправкою на відповідні зрушення:

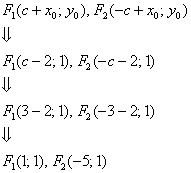
Тут все обходиться значно простіше, ніж при повороті, і якщо за умовою не потрібно приводити рівняння до канонічного виду, то особисто я вважатиму за краще залишити його у вигляді 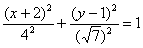. Що робити, якщо потрібно приводити? «Чайникам» в більшості випадків пробачать фразу: «Здійснимо паралельний перенос еліпса в початок координат і перепишемо рівняння 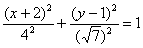в канонічному вигляді: 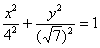». Але академічний підхід передбачає паралельний перенос не самої фігури, а системи координат! Тому людям, що вивчають вищу математику за профілем і / або поглиблено, набагато краще загорнути приблизно наступне: «За допомогою паралельного перенесення вихідної системи координат перейдемо до нової прямокутної системі координат 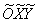з початком в точці 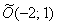і запишемо рівняння еліпса в канонічному вигляді ».

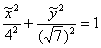Насправді спрощена версія формули нам знайома ще зі шкільних часів:

рівняння 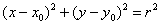задає коло радіуса 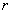з центром в точці .

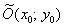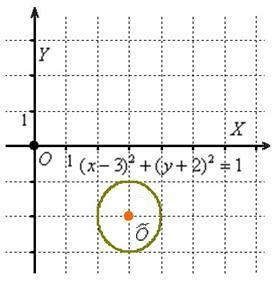
Освіжаючи ностальгічні спогади, зобразимо на кресленні окружність, задану рівнянням :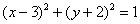

У дослідницьких цілях наведемо наше рівняння до загального вигляду, виконавши зведення в квадрат і приведення подібних доданків: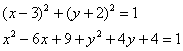

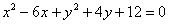- як правило, в такому вигляді воно і зустрічається в природі.

Таким чином, в практичних завданнях часто попередньо потрібно виконати зворотну дію - виділити повні квадрати. Даний прийом докладно розібраний на уроках про геометричних перетвореннях графіків и інтегруванні дробів . Хоча наступний простий приклад не повинен викликати у вас труднощів навіть без відпрацювання даного методу:

приклад 3

Побудувати графік лінії, заданої рівнянням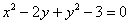

Рішення і креслення в кінці уроку.

На практиці еліпс (як і інші лінії) може бути одночасно повернутий на будь-який кут щодо свого канонічного положення і перенесений в будь-яку точку, відмінну від початку координат. В такому випадку вирішується звичайне завдання приведення лінії 2-го порядку до канонічного вигляду , До якої я потихеньку почав вас готувати вже сьогодні.

Ну а поки самий час перейти до другої частини лекції, де жертвами стануть гіпербола і парабола .

Рішення і відповіді:

Автор: Ємелін Олександр

Вища математика для заочників і не тільки >>>

(Перехід на головну сторінку)