А. Китайгородский

Як вимірюються відстані між атомами в кристалах

Слова «структура», «будова» - дуже ємні за змістом. Різні дослідники розуміють під цими словами різні речі. Біолог може вести мову про структуру м'язової тканини, маючи на увазі розташування волокон один щодо одного; металографія, кажучи про будову сплаву, зазвичай має на увазі форму і розміри зерен. Ці структури спостерігаються за допомогою звичайного мікроскопа при збільшенні всього лише в кілька сотень разів. Але ті ж самі слова використовуються і тоді, коли мова йде про частки, що входять до складу атомного ядра, розміри яких вимірюються трильйонними частками сантиметра. Тут слово «структура» має вже умовний сенс, і фізики користуються ним з обережністю, пам'ятаючи, що наочні зорові уявлення не годяться для таких малих цеглинок світобудови.

У фізиці твердого тіла слова «будова» і «структура» також можуть використовуватися в різних сенсах. Так, наприклад, обговорюючи електронна будова металу, мають на увазі зовсім не розміщення електронів в просторі, а характер розподілу їх по енергіях; кажучи про структуру феромагнітних матеріалів, описують розміри, форму і розташування доменів. Є й інші ситуації, де слово «структура» виявляється досить доречним.

У цій статті мова піде про атомну структуру кристалів, під якою розуміється візерунок, створюваний центрами атомів. Атомна структура визначається рентгеноструктурньїм аналізом, в основі якого лежить явище дифракції рентгенівських променів. За допомогою цього чудового явища, відкритого в 1912 році Максом Лауе, вдається виміряти відстані між центрами атомів твердого тіла і визначити їх взаємне просторове розташування. За 65 років, які пройшли з часу відкриття Лауе, за допомогою рентгеноструктурного аналізу вдалося встановити геометрію розташування атомів приблизно в десятці тисяч кристалів.

Завдання цієї статті полягає в тому, щоб познайомити читача з основними ідеями рентгеноструктурного аналізу і дати уявлення про дорогу, слідуючи якій, можна визначити структуру кристала: виміряти відстані між атомами, дати картину просторового розташування атомів в молекулі і упаковку молекул в кристалі і т.п . Вирішуючи цю задачу, ми, природно, гранично спростимо її. Наша мета - повторимо ще раз - зробити ясними принципи, що лежать в основі методу.

На малюнку 1 зображена атомна структура кристала йодистой ртуті. Молекула цієї речовини складається з одного атома ртуті і двох атомів йоду. Атоми, що утворюють кристал, розташовані так, як деталі малюнка шпалер. Якщо розфарбувати фігурки, відповідні атомам різних сортів, в різні кольори, то вийдуть шпалери. Може бути, з естетичної точки зору вони залишать бажати кращого, але принцип шпалер буде в наявності: можна виділити елементарну комірку, періодичним зміщенням якої в двох напрямках «будуються» шпалери. Про шпалери можна сказати, що вони представляють двовимірну решітку. Видаліть подумки всі деталі малюнка, крім ліній, і справедливість попередньої фрази стане очевидною. Точки перетину ліній називають вузлами.

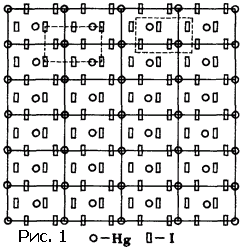
Вибір вузлів і, відповідно, ліній решітки, довільний. Проте існують деякі правила вибору вузлів. Справа в тому, що від вузла решітки відраховуються координати атомів, а тому природно вибрати вузол в симетричній точці. З трьох, зазначених на малюнку 1 варіантів (з незліченної безлічі можливих), ми вважали за краще найбільш доцільний.

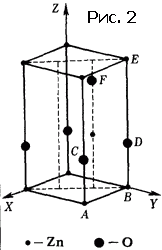
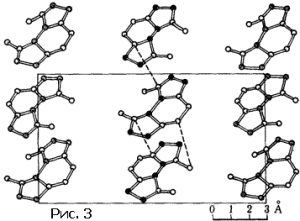
Ми погрішили проти істини, сказавши, що на малюнку 1 зображена структура кристала. Насправді показана проекція структури на площину. Кристал - тривимірні шпалери. Решітка кристали не двовимірна, а тривимірна. Осередок - чи не параллелограмм або прямокутник, а паралелепіпед. Він може бути прямокутним, а в деяких випадках - виродитися в куб. Осередок може містити один, два атома, а в складних випадках - сотні і тисячі. Зрозуміло, що дослідник, який бажає познайомити читача своєї статті зі структурою вивченого кристала, обмежиться тим, що зобразить вид в перспективі одного осередку. На малюнку 2 показана структура дуже простого кристала (окису цинку), а на малюнку 3 - складного органічного з'єднання.

Ви познайомилися з мінімальними відомостями, необхідними для того, щоб розібратися в суті рентгеноструктурного аналізу. Принцип цього найпотужнішого способу вивчення речовини полягає в реєстрації вторинного рентгенівського випромінювання, яке виходить від всіх атомів кристала, коли на нього падає первинний вузький пучок рентгенівських променів. Намагаються підібрати умови досвіду такими, щоб кристал був прозорий для променів. Тоді в створенні розсіяного випромінювання (вторинного, діфрагованого - це все синоніми) братимуть участь всі атоми кристала.

Явище, про яке йде мова, далеко не просте. Але нам немає потреби входити в деталі. Тому всі проблеми будуть розглянуті на гранично простому прикладі. Перше спрощення - обмежимося вивченням проекції структури кристала, друге - будемо розглядати прямокутну решітку, третє - покладемо, що на осередок доводиться одна двухатомная молекула.

Спочатку займемося описом «порожній решітки», з якої атоми «видалені». Залишилися одні вузли. Батько і син Брегг показали, що дифракцию рентгенівських променів можна розглядати як своєрідне виборче (тобто те, що відбувається лише при деяких дискретних значеннях кута) відображення променів від систем вузлових площин, на які може бути розбита решітка.

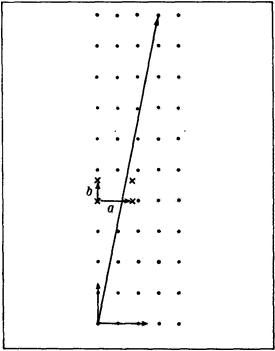
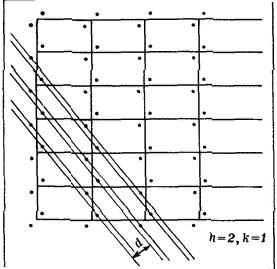
Ясно, що просторова решітка кристала може бути розбита на сімейства вузлових площин різними шляхами. На картині проекції «звільненій» від атомів решітки легко показати сліди вузлових площин, перпендикулярних до площини креслення (рис. 4). Ми зобразили всього лише п'ять родин площин. Однак ефективними для виборчого відображення, сутність якого буде описана нижче, є кілька десятків, а то і сотень площин.

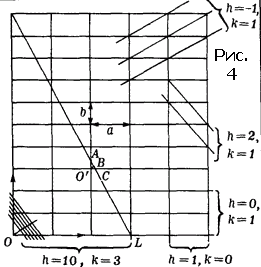
Кожна система площин характеризується індексами h і k. Їхній зміст ілюструється на прикладі сімейства з індексами h = 10 і k = 3 (див. Рис. 4). Щоб не захаращувати креслення, ми побудували шість найближчих до вузла O площин і провели ще одну, позначену L. Площина L є найближчою до вузла O, відтинає ціле число періодів a і b по обох осях решітки. Ці цілі числа рівні 3 по одній осі і 10 по інший. Проходячи через осередок O ', площина L відсікає 1/10 частку періоду a і 1/3 періоду b. Сенс індексів h і k стає очевидним. Надаємо вам самим скласти фразу такого типу, як люблять математики: «Індексами h і k називаються ...».

Системи площин характеризуються також межплоскостним відстанню d. Площина L - найближча до вузла O ', тому | O'B | = d. відрізки | O'A | і | O'C | можна записати, як b / k і a / h. оскільки

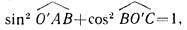
отримаємо

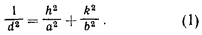
(Пропонуємо вам вирішити чудову завдання, яка забере у вас не одну годину часу - виведіть аналогічну формулу для тривимірної решітки, осередок якої є косокутних параллелепипедом.)

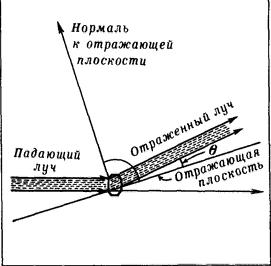
Переходимо до висновку основного закону селективного (виборчого) відображення рентгенівських променів кристалом. Нехай падаючий промінь, який представляє собою електромагнітну хвилю певної довжини λ, падає на кристал під якимось кутом. Ми маємо право вважати, що відображення рентгенівської хвилі буде відбуватися згідно із законом: кут падіння дорівнює куту відбиття, тобто за таким же законом, як і для оптичного променя. Але є велика різниця з оптичним променем. Промінь світла не проникає в глиб кристала, а рентгенівський промінь здатний пройти крізь кристал. Це означає, що відображення рентгенівського променя відбуватиметься не тільки від зовнішньої поверхні кристала, а від усіх його атомних площин.

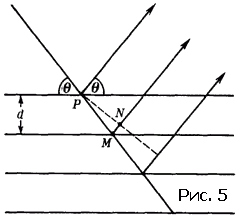
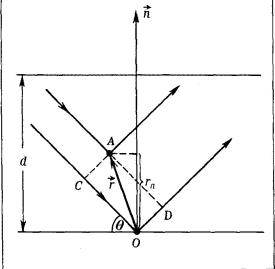
Розглянемо одну з систем, що характеризуються межплоскостним відстанню d (рис. 5). Кожна з площин буде відображати падаючий промінь під одним і тим же кутом θ (так званий кут дифракції). Ці відбиті промені когерентні, а тому долждни интерферировать між собою. Причому вторинні (відображені) промені будуть підсилювати один одного в тому випадку, якщо після відображення від всіх площин сімейства вони будуть поширюватися в одній фазі. Іншими словами, якщо різниця ходу між променями дорівнює цілому числу n довжин хвиль. Різниця ходу | PM | + | MN | (див. рис. 5) між сусідніми відбитими променями дорівнює 2 d sin θ (доведіть!). Отже умова дифракції - умова посилення відбитих променів - матиме вигляд

2 d sin θ = n λ (2)

Воно носить назву рівняння Брегга.

Кристал, як ми вже сказали, можна розбити на системи площин нескінченним числом способів. Але ефективної для відображення (тепер вам зрозумілий сенс цих слова, чи не так?) Виявиться лише система площин з таким межплскостним відстанню і орієнтована так по відношенню до падаючого променю, щоб виконувалося рівняння Брегга.

Якщо падаючий промінь монохроматический (тобто електромагнітна хвиля має одну певну довжину), то при довільному положенні кристала по відношенню до променя відображення може і не статися (вірніше, сумарний ефект безлічі відображень може виявитися нульовим). Однак, повертаючи кристал, ми можемо по черзі привести в відбиває стан різні системи площин. Саме такий спосіб роботи і виявився на практиці найбільш підходящим.

З рівняння Брегга (рівняння (2)) випливає, що для заданої довжини хвилі існує мінімальне значення відстані d між площинами, при якому можливе селективне відображення. Це відстань λ / 2 (оскільки синус не може бути більше одиниці). З іншого боку, з наведеної вище формули міжплощинних відстаней (формула (1)) ясно, що найбільшим значенням d відповідають найменші значення h і k.

Здебільшого при рентгеноструктурном аналізі використовується одна з довжин хвиль характеристичного випромінювання міді, а саме 1,54 ангстрема [1] . Тоді найменші межплоскостним відстані, здатні взяти участь у створенні дифракційної картини, рівні 0,77 ангстрема. Маючи в своєму розпорядженні цими відомостями, можна оцінити, скільки систем площин дадуть відображення, якщо відомі періоди решітки a і b. Спробуйте вирішити цю задачу геометрично для a = 10 і b = 20 Ангстрема.

Для цієї мети треба провести коло радіуса 1 / λ в просторі (в нашому двовимірному випадку - в площині) «зворотної» решітки. І далі підрахувати число ... (чого, здогадайтеся). Але що таке «зворотна» решітка і навіщо нам знадобилося це нове поняття?

У нашому випадку зворотного гратами називається решітка, осередок якої є прямокутник зі сторонами 1 / a і 1 / b. Як бачите, прикметник «зворотна» цілком доречно. На малюнку 6 побудована така решітка. Виберемо початок координат в будь-якому вузлі і проведемо осі координат - одну перпендикулярно до осі кристала, по якій період дорівнює a, другу перпендикулярно до осі з періодом b. Проведемо тепер в цій решітці вектор (він так і називається: вектор оберненої гратки), який з'єднує початок відліку з вузлом оберненої гратки, номер якого 10-й по одній осі, і 3-й по інший. Чому дорівнює довжина цього вектора? Повернемося до рівняння (1) для межплоскостним відстані і без праці і з цікавістю зауважимо, що довжина вектора дорівнює 1 / d для системи площин з h = 10 і k = 3.

Але цього мало. Легко довести (доведіть), що проведений вектор оберненої гратки перпендикулярний до системи площин, для яких h = 10, k = 3. І, звичайно, це справедливо для будь-якого вузла номера h, k. А як закінчиться справа, якщо номер вузла містить кратний множник n? Відповідь очевидна - в цьому випадку довжина вектора оберненої гратки буде дорівнювати n / d.

Ось тепер ми маємо в своєму розпорядженні усіма неободимого відомостями для того, щоб повернутися до досвіду. У чому ж полягає експеримент? Кристал встановлюється на спеціальний утримувач так, щоб одна з його осей (одне з ребер його елементарної комірки) була вертикальною, і повертається близько цієї осі. Таким способом ми по черзі підставляємо в «відбиває» положення все системи вузлових площин кристала. Для того щоб «зловити» відбитий промінь, можна вдатися або до фотографічному методу, або використовувати іонізаційну камеру, лічильник Гейгера або інший прилад, реєструючий іонізуюче випромінювання.

Зараз, зрозуміло, все це робиться автоматично, а в той час, коли ми починав працювати, процедура була такою. Встановлювався кристал, потім приймач вторинного променя провертався у всьому діапазоні улов. Око стежив при цьому за що показує струм приладом. Потім кристал повертався, скажімо, на один градус, і далі ці дії повторювалися доти, поки ми не «натикалися» на відбитий промінь. При цьому, як видно з малюнка 7, фіксувалися два кута - значення бреггівського кута θ і положення нормалі до відображає площині (по відношенню до будь-якого довільного початку відліку).

Перед дослідником лежав аркуш паперу, і він починав будувати зворотний грати. Відкладав положення нормалі до відображає площині і наносив на лінію цієї нормалі значення n / d, яке однозначно визначалося з рівняння Брегга. Коли ця робота закінчувалася (в старі добрі часи вона займала місяці, а зараз автоматичний дефрактометр виконує її в сотні разів швидше), фізик знаходив картину оберненої гратки. З її осередки він негайно з'ясовував розміри осередку кристала, а кожному відображенню міг приписати номер вузла оберненої гратки, а значить, індекси h і k і порядок відображення n.

Крім того, досліднику відомі інтенсивності всіх відображень. Таким чином, в його розпорядженні є практично всі відомості про структуру кристала, все, що стосується характеру будови молекули з атомів і кристала з молекул.

Тепер нам треба перейти від «порожній» решітки, що складається з одних вузлів, до ґрат, начиненою атомами. На яких деталях дифракційної картини позначається структура осередку? Відповідь виявиться таким: структура осередку впливає на інтенсивність відбитих променів. Що ж стосується геометрії дифракційної картини, то вона визначається тільки видом решітки. Атоми всередині осередку не додають «зайвих» відбитих променів. У той же час цілком можливо, що структура осередку змусить прірву деякі відображення - доведе їх інтенсивність до нуля.

Звідки випливає такий висновок? Справа в тому, що атоми всередині комірки не створять нових систем площин. Візерунок атомів призведе лише до виникнення «вставних» площин. Погляньте, на малюнку 8 зображена та ж решітка, що і на малюнку 4. Але тепер вона не «порожня». Виберемо знову гранично простий випадок. Припустимо, що реальна решітка побудована з двохатомних молекул, а вузол решітки був узятий в центрі такої молекули. Реальна система площин (для прикладу взято випадок h = 2 і k = 1) буде виглядати тепер, як і показано на малюнку 8. Відбитий промінь піде в ту ж сторону, бреггівськими кут не зміниться.

Покажемо, що інтенсивність відбитого променя буде залежати від структури осередку - в даному випадку від міжатомної відстані в молекулі і від кута, який утворює вісь молекули з віссю осередки.

Інтенсивність випромінювання пропорційна квадрату амплітуди хвилі. Дійсно, нехай в точці спостереження поле, створюване гратами атомів, записується як A cos ω t. інтенсивність дорівнює

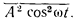
Риска зверху означає усереднення за часом (коливання відбуваються швидко, і досвід фіксує середні значення). але

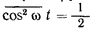
(Це нескладно довести). Тому інтенсивність виявляється пропорційною A ² - квадрату амплітуди хвилі.

У разі решітки двоатомних молекул результуючий поле електромагнітної хвилі можна розглядати як суму полів двох простих решіток. Ці два поля прийдуть в точку спостереження із зсувом фаз, який ми позначимо 2α. Зберігаючи вираз A cos ω t для решітки вузлів, ми запишемо тепер суму полів двох решіток у вигляді

A cos (ω t + α) + A cos (ω t -α).

Кожен вузол «розщепився» на дві частинки, що створюють одне поле з випередженням по фазі, а інше з відставанням. Складаючи, зводячи в квадрат і усредняя за часом, ми отримаємо, що інтенсивність відбитого променя буде пропорційна cos²α.

За визначенням,

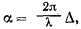
де λ - довжина хвилі, а Δ - різниця ходу. Хоча висновок вираження для різниці ходу Δ нітрохи не відрізняється від виведення формули Брегга, ми все ж для цього випадку провели акуратне побудова на малюнку 9, з якого читач, злегка помучитися, знайде потрібний вираз:

Δ = | OC | + | OD | = 2rn sin θ.

Де rn - проекція радіуса-вектора

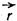
(З'єднує атоми молекули) на напрямком поширення відбитої хвилі (на напрям нормалі

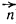
), Θ - бреггівськими кут розсіювання. Використовуємо рівняння Брегга і визначення зворотного вектора:

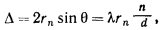
звідки різниця фаз

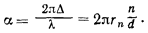
Отже, інтенсивність відбитої хвилі, пропорційна cos²θ, дійсно визначається структурою елементарного осередку кристала. Очевидно, що якщо атомів в комірці не два, а багато, то всі міркування будуть аналогічними.

Що ж ... завдання вірішена? Інтенсівності діфрагірованніх променів пов'язані зі структурою в общем-то простою формулою: розрахунок інтенсівностей відбітіх променів по заданій структурі НЕ складаний. Справа зводиться до того, щоб визначити різниці ходу між хвилями, відбитими усіма «вставними» гратами. Ви можете впоратися з цим завданням і для кристала, що складається із сотні атомів. Питання лише в часі.

Але читач, безсумнівно, помітив, що розрахунок, про який йде мова, не той, який нам потрібен. Завдання полягає в знаходженні атомної будови з даних досвіду, а не в тому, щоб розрахувати дифракційну картину, виходячи з відомостей про структуру. Пряма задача набагато складніше зворотного. Інтенсивність пропорційна квадрату амплітуди результуючої хвилі, яка є сума тригонометричних функцій. Не тільки технічно складно, але і просто неможливо визначити аргументи косинусів, знаючи лише квадрат їх сум. Ось якби досвід давав значення амплітуд розсіювання, тоді справа йшла б зовсім просто.

На перший погляд ситуація здається безнадійною. Довгий час дослідники діяли так званим методом проб і помилок. Це означає: придумували структуру і дивилися, чи поєднується вона з досвідом. Але так далеко не заїдеш.

Були придумані способи обійти ці труднощі. Вирішальну роль при цьому зіграли електронно-обчислювальні машини. Хотілося б дати читачеві ідею про те, як ці труднощі обходиться, але розмова наша про рентгеноструктурном аналізі затягнувся. «Маленькі хитрощі», до яких вдаються дослідники, це, по-перше, введення в структуру важкого атома (тоді в першому наближенні можна вважати, що кристал складається з одних цих атомів) і, по-друге, дуже витончена теорія, яка показує, що між різними структурними амплітудами є зв'язку.

Так, добре було б розповісти про це читачеві, але для «Кванта» бесіда була б занадто довгою. Тому нічого не залишається, як порадити цікавиться читачеві звернутися до спеціальної літератури.

Про успіхи методу судять за його результатами. Та обставина, що на сьогодні визначені структури більше 15 тисяч кристалів, в тому числі кілька десятків структуро білків, молекули яких складаються з багатьох тисяч атомів, говорить сама за себе. Визначення структури складних молекул закладає фундамент біологічної хімії та біолоіческой фізики. Ці науки знаходяться зараз в бурхливому періоді розвитку. Від них чекають відкриття секретів життя, хвороб і смерті. Рентгеноструктурний аналіз, незважаючи на свій солідний шістдесятип'ятирічний вік, залишається на передній лінії фронту науки.