Статист і чний ан а ліз в чому е рний, в широкому сенсі - розділ математичної статистики , Який об'єднує методи вивчення статистичних даних, що відносяться до об'єктів, які характеризуються декількома якісними або кількісними ознаками. Найбільш розроблена частина С. а. м., заснована на припущенні, що результати окремих спостережень незалежні і підпорядковані одному і тому ж багатовимірному нормальному розподілу (Зазвичай саме до цієї частини застосовують термін С. а. М. У вузькому сенсі). Іншими словами, результат Xj спостереження з номером j можна представити вектором

Xj = (Xj1, Xj2, ..., Xjs),

де випадкові величини Xjk мають математичне очікування m k, дисперсію s 2k, а коефіцієнт кореляції між Xjk і Xjl дорівнює r kl. Вектор математичних очікувань m = (m 1, ..., m s) і ковариационная матриця S з елементами s k s l r kl, k, l = 1, ..., s, є основними параметрами, повністю визначають розподіл векторів X1 , ..., Xn - результатів п незалежних спостережень. Вибір багатовимірного нормального розподілу в якості основної математичної моделі С. а. м. частково може бути виправданий наступними міркуваннями: з одного боку, ця модель є прийнятною для великого числа додатків, з іншого - тільки в рамках цієї моделі вдається обчислити точні розподілу вибіркових характеристик. вибіркове середнє 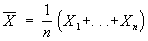і вибіркова ковариационная матриця

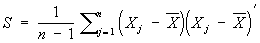
[де 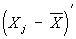позначає транспонований вектор 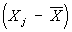, См. матриця ] Суть оцінки максимальної правдоподібності відповідних параметрів сукупності. розподіл 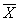нормально 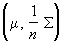, А спільний розподіл елементів ковариационной матриці S, т. Н. розподіл Уішарт, є природним узагальненням «Хі-квадрат» розподілу і відіграє значну роль в С. а. м.

Ряд завдань С. а. м. більш-менш аналогічний відповідним одновимірним завданням (наприклад, завдання перевірки гіпотез про рівність середніх значень в двох незалежних вибірках). Іншого типу завдання пов'язані з перевіркою гіпотез про незалежність тих чи інших груп компонент векторів Xj, перевіркою таких спеціальних гіпотез, як гіпотеза сферичної симетрії розподілу Xj і т.д. Необхідність розібратися в складних взаємозв'язках між компонентами випадкових векторів Xj ставить нові проблеми. З метою скорочення числа розглянутих випадкових ознак (зменшення розмірності) або зведення їх до незалежних випадкових величин застосовуються метод головних компонент і метод канонічних кореляцій. В теорії головних компонент здійснюється перехід від векторів Xj до векторів Yj = (Yj1, ..., Yjr). При цьому, наприклад, Yj1 виділяється максимальною дисперсією серед всіх нормованих лінійних комбінацій компонент X1; Yj2 має найбільшу дисперсію серед всіх лінійних функцій компонент X1, що не корелюється з Yj1 і т.д. У теорії канонічних кореляцій кожне з двох множин випадкових величин (компонент Xj) лінійно перетвориться в нове безліч т. Н. канонічних величин так, що всередині кожного безлічі коефіцієнти кореляції між величинами дорівнюють 0, перші координати кожної безлічі мають максимальну кореляцію, другі координати мають найбільшу кореляцію з решти координат і т.д. (Впорядковані т. О. Кореляції називаються канонічними). Останній метод вказує максимальну кореляцію лінійних функцій від двох груп випадкових компонент вектора спостереження. Висновки методів головних компонент і канонічних кореляцій допомагають зрозуміти структуру досліджуваної багатовимірної сукупності. Подібним цілям служить і факторний аналіз , В схемі якого передбачається, що компоненти випадкових векторів Xj явлются лінійними функціями від деяких спостережених чинників, що підлягають вивченню. В рамках С. а. м. розглядається і проблема диференціації двох або більшого числа совокупностей за результатами спостережень. Одна частина проблеми полягає в тому, щоб на основі аналізу вибірок з декількох сукупностей віднести новий елемент до однієї з них (дискримінація), інша - в тому, щоб усередині сукупності розділити елементи на групи, в певному сенсі максимально відрізняються один від одного.

Літ .: Андерсон Т., Введення в багатомірний статистичний аналіз, пров. з англ., М., 1963; Kendall М. G., Stuart А., The advanced theory of statistics, v. 3, L., 1966; Dempster AP, Elements of continuons multivariate analysis, L., 1969.

А. В. Прохоров.