Галіл е я пр і нціп відносять і ності, принцип фізичного рівноправ'я інерційних систем відліку в класичній механіці, який проявляється в тому, що закони механіки у всіх таких системах однакові. Звідси випливає, що ніякими механічними дослідами, що вживаються в будь-якої інерціальній системі, не можна визначити, спочиває чи ця система або рухається рівномірно і прямолінійно. Це положення було вперше встановлено Г. Галілеєм в 1636. Подібність законів механіки для інерціальних систем Галілей ілюстрував на прикладі явищ, що відбуваються під палубою корабля, покоїться або рухається рівномірно і прямолінійно (щодо Землі, яку можна з достатнім ступенем точності вважати інерціальній системою відліку): «Примусьте тепер корабель рухатися з будь-якою швидкістю і тоді (якщо тільки рух буде рівномірним і без качки в ту і іншу сторону) у всіх названих явищах ви не знайдете ні найменшого зміни і по жодному з них не зможете встановити, чи рухається корабель або стоїть нерухомо ... Кидаючи яку-небудь річ товаришеві, ви не повинні будете кидати її з більшою силою, коли він буде перебувати на носі, а ви на кормі, ніж коли ваше взаємне положення буде зворотним; краплі, як і раніше, будуть падати в нижній посудину, і жодна з них не впаде ближче до корми, хоча, поки крапля знаходиться в повітрі, корабель пройде багато п'ядей »(« Діалог про дві найголовніші системи світу птоломєєвой і коперниковой », М. - Л., 1948, с. 147).

Рух матеріальної точки відносно: її положення, швидкість, вид траєкторії залежать від того, по відношенню до якої системи відліку (тілу відліку) цей рух розглядається. У той же час закони класичної механіки (див. Ньютона закони механіки ), Т. Е. Співвідношення, які пов'язують величини, що описують рух матеріальних точок і взаємодія між ними, однакові у всіх інерціальних системах відліку. Відносність механічного руху і однаковість (безвідносність) законів механіки в різних інерціальних системах відліку і складають зміст Г. п. О.

Математично Г. п. О. висловлює інваріантність (незмінність) рівнянь механіки відносно перетворень координат рухомих точок (і часу) при переході від однієї інерціальної системи до іншої - перетворень Галілея.

Нехай є дві інерціальні системи відліку, одну з яких, S, домовимося вважати спочиває; друга система, S ', рухається по відношенню до S з постійною швидкістю u так, як показано на малюнку. Тоді перетворення Галілея для координат матеріальної точки в системах S і S 'матимуть вигляд:

x '= x - ut, у' = у, z '= z, t' = t (1)

(Штриховані величини відносяться до системи S ', нештріхованние - до S). Т. о., Час у класичній механіці, як і відстань між будь-якими фіксованими точками, вважається однаковим у всіх системах відліку.

З перетворень Галілея можна отримати співвідношення між швидкостями руху точки і її прискореннями в обох системах:

v '= v - u, (2)

a '= a.

У класичній механіці рух матеріальної точки визначається другим законом Ньютона:

F = ma, (3)

де m - маса точки, a F - рівнодіюча всіх доданих до неї сил. При цьому сили (і маси) є в класичній механіці інваріантами, т. Е. Величинами, які не змінюються при переході від однієї системи відліку до іншої. Тому при перетвореннях Галілея рівняння (3) не змінюється. Це і є математичний вираз Г. п. О.

Г. п. О. справедливий лише в класичній механіці, в якій розглядаються руху зі швидкостями, багато меншими швидкості світла. При швидкостях, близьких до швидкості світла, рух тіл підкоряється законам релятивістської механіки Ейнштейна (див. відносності теорія ), Які інваріантні по відношенню до інших перетворень координат і часу - Лоренца перетворенням (При малих швидкостях вони переходять в перетворення Галілея).

В. І. Григор'єв.

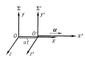
Інерціальна система відліку S '(з координатними осями x', y ', z') рухається відносно іншої інерціальної системи S (з осями х, у, z) в напрямку осі х з постійною швидкістю u. Координатні осі обрані так, що в початковий момент часу (t = 0) відповідні осі координат збігаються в обох системах.