регулювання автоматичне
Регул і вання автомат і чеський (від нім. Regulieren - регулювати, від лат. Regula - норма, правило), підтримання сталості (стабілізація) деякої регульованої величини, що характеризує технічний процес, або її зміну по заданому закону (програмне регулювання) або відповідно з деяким що вимірюється зовнішнім процесом (що стежить регулювання), здійснюване додатком дії, що управляє до регулюючого органу об'єкта регулювання; різновид автоматичного управління . При Р. а. керуючий вплив u (t) зазвичай є функцією динамічної помилки - відхилення e (t) регульованої величини х (t) від її заданого значення x 0 (t): e (t) = x 0 (t) - х (t) (принцип Ползунова - Уатта регулювання по відхиленню, або принцип зворотнього зв'язку ) (Рис., А). Іноді до Р. а. відносять також управління, при якому u (t) виробляється (пристроєм компенсації) у функції впливу, що обурює f (навантаження) на об'єкт (принцип Понселе регулювання по обуренню) (рис., б), і комбіноване регулювання по відхиленню і обуренню (рис., б).
Для здійснення Р. а. к. об'єкту підключається комплекс пристроїв, що представляють собою в сукупності регулятор . Об'єкт і регулятор утворюють систему автоматичного регулювання (CAP). САР за відхиленням є замкнутої (див. Замкнута система управління ), По обуренню - розімкнутої (див. Разомкнутая система управління ). Математичне вираження функціональної залежності бажаного (запланованого) керуючого впливу u 0 (t) від вимірюваних регулятором величин називається законом, або алгоритмом , Регулювання. Найбільш часто застосовуються закони Р. а .: П - пропорційний (статичний), u 0 = k e, І - інтегральний (астатичний), 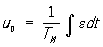 ; ПІ - пропорційно-інтегральний (ізодромний),
; ПІ - пропорційно-інтегральний (ізодромний), 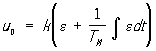 , ПІД - пропорційно-інтегральний з похідною,
, ПІД - пропорційно-інтегральний з похідною, 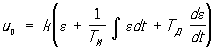 ; тут k - коеффіциет посилення регулятора, Т і і тд - постійні часу інтегрування і диференціювання. Фактична дія u (t) відрізняється від u 0 (t) внаслідок інерційності регулятора. CAP є динамічною системою , Процеси в якій описуються диференціальними, диференціально-різницевими і т. П. Рівняннями.
; тут k - коеффіциет посилення регулятора, Т і і тд - постійні часу інтегрування і диференціювання. Фактична дія u (t) відрізняється від u 0 (t) внаслідок інерційності регулятора. CAP є динамічною системою , Процеси в якій описуються диференціальними, диференціально-різницевими і т. П. Рівняннями.
САР може знаходитися в стані рівноваги, в ній можуть протікати сталі і перехідні процеси, кількісні характеристики яких вивчає теорія автоматичного регулювання (ТАР). В статичних системах регулювання встановилася похибка (помилка) e ст при постійному навантаженні (на об'єкт) залежить від величини останньої. Для підвищення статичної точності збільшують коефіцієнт посилення регулятора k, але при досягненні ним деякого критичного значення k kp система зазвичай втрачає стійкість . Введення в регулятор інтегруючих елементів дозволяє отримати астатическую систему регулювання , В якій при будь-якої постійної навантаженні статична помилка відсутня. ТАР вивчає умови стійкості, показники якості процесу регулювання (динамічну і статичну точність, час регулювання, коливальність системи, ступінь і запаси стійкості і т. П.) І методи синтезу CAP, т. Е. Визначення структури і параметрів коригувальних пристроїв, що вводяться в регулятор для підвищення стійкості і забезпечення необхідних показників якості Р. а.
Найбільш повно розроблена ТАР лінійних систем, в якій застосовуються аналітичні і частотні методи дослідження. Малі відхилення від рівноважних станів в безперервних нелінійних системах Р. а. досліджуються за допомогою лінеаризації вихідних рівнянь. Процеси при великих відхиленнях і специфічних особливості; нелінійних CAP (граничні цикли, автоколивання, загарбання, ковзаючі режими і т. п.) вивчаються методами фазового простору . Для вивчення періодичних режимів також застосовують наближені методи малого параметра, гармонія, балансу та ін. Стійкість при великих відхиленнях досліджується другим (прямим) методом Ляпунова і методом абсолютної стійкості, розробленим: В. М. Поповим (Румунія). Спеціальний розділ ТАР присвячений Р. а. при випадкових впливах.
З 50-х рр. 20 в. розвиваються теорія інваріантних CAP, що забезпечують незалежність х (t) від збурень, і теорія багатозв'язних CAP, в яких багато величини пов'язані через регульований об'єкт. У таких CAP часто вводять додаткові зв'язки між регуляторами з метою отримання певних властивостей, зокрема автономності (Незалежності процесів регулювання окремих величин). У 60-х рр. отримала розвиток і застосування теорія систем зі змінною структурою, особливо ефективних при роботі в умовах великих змін параметрів системи і середовища, т. к. перехідні процеси в них визначаються властивостями керуючого пристрою і мало залежать від параметрів об'єкта регулювання і середовища.
Особливе місце в ТАР займають дискретні системи Р. а., В яких здійснюється квантування сигналу . З них найбільш вивчені імпульсні системи (З квантуванням за часом), релейні системи (З квантуванням за рівнем) і цифрові системи (З квантуванням за часом і рівнем). Приватний вид релейних систем - двохпозиційні регулятори , В яких регулюючий орган може займати лише одне з двох крайніх положень.
Історія розвитку Р. а. Дати винаходу перших регулюючих пристроїв, так само як і імена їх винахідників, не встановлені. Наприклад, поплавковий регулятор рівня водяного годинника, заснований на принципі регулювання по відхиленню, був відомий арабам ще в початку н. е. На борошномельних млинах в середні століття застосовувалися відцентрові маятники для регулювання частоти обертання жорен. Однак першими регуляторами, які отримали широке практичне застосування в промисловості, стали регулятор живлення котла парової машини І. І. Ползунова (1765) і відцентровий регулятор частоти обертання парової машини Дж. Уатта (1784).
Перші регулятори здійснювали пряме регулювання, при якому вимірювальний орган безпосередньо впливав на регулюючий орган. Таке Р. а. було можливо тільки на машинах малої потужності, де для переміщення регулюючих органів (важеля, колеса) не вимагалося великих витрат енергії. У 1873 французький інженер Ж. Фарко вперше здійснив непряме Р. а., Ввівши в ланцюг регулювання підсилювач - гідравлічний сервомотор з жорсткою зворотним зв'язком. Це дало можливість не тільки підвищити потужність впливу регулятора, а й отримати більш гнучкі алгоритми Р. а. У 1884 з'явився регулювальник непрямої дії з додатковою релейного зворотним зв'язком, що діяла до тих пір, поки відхилення було відмінно від нуля. Потім релейний зв'язок була замінена безперервної диференціальним зв'язком, що отримала назву ізодромною.
З 2-ї половини 19 ст. Р. а. застосовується в самих різних технічних устройствах- парових котлах, компресорних установках, електричних машинах і ін. До цього ж періоду відноситься і становлення науки про Р. а. У статті Дж. К. Максвелла «Про регулювання» (1868) вперше розглянута математична задача про стійкість лінійної CAP. Працею І. А. Вишнеградський «Про регуляторах прямої дії» (1877) закладена основа ТАР як нової науково-технічної дисципліни. Подальше її розвиток і систематичний виклад дано А. Стодоля , Я. І. Грдіна і Н. Е. Жуковським .
Новий етап в розвитку Р. а. настав з застосуванням в регуляторах електронних елементів, зокрема обчислювальних пристроїв, що істотно розширило можливості покращити алгоритмів регулювання введенням впливів по вищим похідним, интегралам і більш складних функцій. Переваги електронних регуляторів особливо проявилися в самоналагоджувальних системах , Першими з яких були екстремальні регулятори : Регулятор топки парового котла (1926), електричний регулятор ккд (1940), авіаційні регулятори (1944). Однак подібні регулятори застосовують лише в найпростіших випадках, наприклад для підтримки екстремуму функції однієї змінної. У більш складних САР доцільно розділити систему регулювання на дві частини: обчислювальний пристрій, що визначає оптимальну настройку регулятора, і власне регулятор. У складних системах управління Р. а. використовується лише на нижчому щаблі ієрархічного управління - регулятори впливають безпосередньо на керований об'єкт, будучи виконавцями команд ЕОМ (або операторів), що знаходяться на вищих щаблях управління.
Літ .: Теорія автоматичного регулювання, під ред. В. В. Солодовникова, книга 1-3, М., 1967-69; Воронов А. А., Основи теорії автоматичного управління, ч. 1-3, М. - Л., 1965-70; Заде Л., Дезоер Ч., Теорія лінійних систем. Метод простору станів, пров. з англ., М., 1970; Бесекерскій В. А., Попов Е, П., Теорія систем автоматичного регулювання, М., 1972; Сю Д., Мейєр А., Сучасна теорія автоматичного управління і її застосування, пер. з англ., М., 1972; Основи автоматичного управління, під ред. В. С. Пугачова, 3 вид., М., 1974.
А. А. Воронов.

Структурні схеми автоматичного регулювання по відхиленню (а), по обуренню (б) і комбінованого (в): x0 - задане значення регульованої величини; e - динамічна помилка (неузгодженість); u - керуючий вплив; f - рівноваги вплив (навантаження); x - регульована величина; гуртком, розділеним на сектори, позначений порівнює пристрій.
